Tìm a biết :a√16x =9
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CD
5
4 tháng 5 2015
16 gì vậy bạn
đúng đi bạn đi mà bạn viết lại đề đi khó hiểu lắm
4 tháng 5 2015
16x4-9=0
=>16x4 =0+9
=>16x4 =9
=>x4 =9/16
Đề này khó hiểu quá mình chỉ giải được đến đó thôi+++++
PQ
1
CM
3 tháng 3 2017
a) √16x = 8 (điều kiện: x ≥ 0)
⇔ 16x = 82 ⇔ 16x = 64 ⇔ x = 4
(Hoặc: √16x = 8 ⇔ √16.√x = 8
⇔ 4√x = 8 ⇔ √x = 2 ⇔ x = 4)
b) điều kiện: x ≥ 0
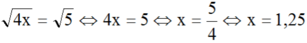
c) điều kiện: x - 1 ≥ 0 ⇔ x ≥ 1 (*)
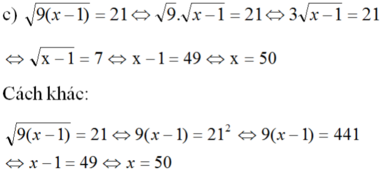
x = 50 thỏa mãn điều kiện (*) nên x = 50 là nghiệm của phương trình.
d) Vì (1 - x)2 ≥ 0 ∀x nên phương trình xác định với mọi giá trị của x.
- Khi 1 – x ≥ 0 ⇔ x ≤ 1
Ta có: 2|1 – x| = 6 ⇔ 2(1 – x) = 6 ⇔ 2(1 – x) = 6
⇔ –2x = 4 ⇔ x = –2 (nhận)
- Khi 1 – x < 0 ⇔ x > 1
Ta có: 2|1 – x| = 6 ⇔ 2[– (1 – x)] = 6
⇔ x – 1 = 3 ⇔ x = 4 (nhận)
Vậy phương trình có hai nghiệm: x = - 2; x = 4
PL
2
14 tháng 7 2023
a: =>2^4x<2^28
=>4x<28
=>x<7
b: =>5^3x+3<5
=>3x+3<1
=>3x<-2
=>x<-2/3
MT
3
KN
19 tháng 7 2019
a) \(x^3-16x=0\)
\(\Leftrightarrow x\left(x^2-16\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\x^2-16=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=0\\x=\pm\sqrt{16}=\pm4\end{cases}}\)
Vậy \(x\in\left\{0;\pm4\right\}\)
KN
19 tháng 7 2019
b) \(x^2-6x+9=0\)
\(\Leftrightarrow\left(x-3\right)^2=0\)
\(\Leftrightarrow x-3=0\)
\(\Leftrightarrow x=3\)
K
Biết rằng 15x 16x 27 x 28 x A= 72y760 . (A là một số tự nhiên và y là một chữ số chưa biết)
Hãy tìm A
5
HT
27 tháng 1 2021
Tui ko biết đề bài có sai hay ko, bởi hệ số khác nhau thì đặt x ra là được, kết ủa là dương vô cùng, ko tồn tại a và b.
NB
1
TA
26 tháng 4 2023
a) \(x^3-16x=0\)
⇔\(x\left(x^2-16\right)=0\)
⇒\(x=0\) hoặc \(x^2-16=0\)
\(TH_1:x=0\)
\(TH_2:x^2-16=0\) ⇔ \(x^2=16\) ⇔ \(x=\pm4\)
Vậy \(x\in\left\{0;\pm4\right\}\)
b) \(\left(2x+1\right)^2-\left(x-1\right)^2=0\)
⇒ \(2x+1=x-1\)
⇒ \(2x+2=x\)
⇒ \(2\left(x+1\right)=x\) ⇒ x = -2
Vậy x = -2
NB
2
KV
13 tháng 1 2022
\(A=\dfrac{16x^2-1}{16x^2-8x+1}\)
\(=\dfrac{\left(4x-1\right)\left(4x+1\right)}{\left(4x-1\right)^2}\)
a) ĐKXĐ:
\(\left(4x-1\right)^2\ne0\Leftrightarrow4x-1\ne0\Leftrightarrow x\ne\dfrac{1}{4}\)
b) \(A=\dfrac{\left(4x+1\right)\left(4x-1\right)}{\left(4x-1\right)^2}=\dfrac{4x+1}{4x-1}\)
DT
13 tháng 1 2022
a,đkxđ : \(16x^2\ne0\Leftrightarrow x\ne0\)
b, \(\dfrac{16x^2}{1}-\dfrac{1}{16x^2}-\dfrac{8x}{1}+1=\dfrac{256x^4}{16x^2}-\dfrac{1}{16x^2}-\dfrac{128x^3}{16x^2}+\dfrac{16x^2}{16x^2}\)
\(=\dfrac{256x^4-1-128x^3+16x^2}{16x^2}=\dfrac{256x^4-128x^3+16x^2-1}{16x^2}\)
\(=\dfrac{\left(256x^4-128x^3+16^2\right)-1}{16x^2}=\dfrac{16x^2\left(16x^2-8x+1\right)-1}{16x^2}\)
\(=\dfrac{\left(4x\right)^2.\left(\left(4x\right)^2-8x+1\right)-1}{16x^2}=\dfrac{\left(4x\right)^2.\left(4x-1\right)^2-1}{16x^2}\)
\(=\dfrac{\left(16x^2-4x\right)^2-1}{16x^2}=\dfrac{\left(16x^2-4x-1\right)\left(16x^2-4x+1\right)}{16x^2}\)
\(=\dfrac{\left(\left(4x\right)^2-4x-1\right)\left(\left(4x\right)^2-4x+1\right)}{\left(4x\right)^2}\)