Giúp mình với ạ cảm ơn mn nhìu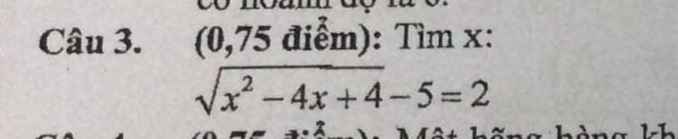
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Câu 2.
Khối lượng riêng của hòn gạch:
\(D=\dfrac{m}{V}=\dfrac{1,6}{\left(1200-2\cdot192\right)\cdot10^{-6}}\approx1961kg/m^3\)
Trọng lượng riêng của gạch:
\(d=10D\approx19610\left(N/m^3\right)\)
Câu 3.
a)Nếu đứng bằng một chân thì áp suất chiếc giày tác dụng lên mặt sàn:
\(p_1=\dfrac{F}{S_1}=\dfrac{P}{S_1}=\dfrac{600}{100\cdot10^{-4}}=60000Pa\)
b)Nếu đứng bằng một chân thì áp suất mỗi chiếc giày tác dụng lên mặt sàn:
\(p_2=\dfrac{F}{S_2}=\dfrac{P}{S_2}=\dfrac{600}{2\cdot100\cdot10^{-4}}=30000Pa\)
Câu 4.
Áp suất của xe tác dụng lên mặt đường:
\(p=\dfrac{F}{S}=\dfrac{26000}{130\cdot10^{-2}}=20000N/m^2\)
Trọng lượng của người đó: \(P=10m=10\cdot45=450N\)
Áp suất của người tác dụng hai chân lên mặt đất:
\(p'=\dfrac{P}{S'}=\dfrac{450}{200\cdot10^{-2}}=225N/m^2\)
Như vậy \(p>p'\).
Câu 5.
a)Áp lực của máy giặt tác dụng lên sàn:
\(F=p\cdot S=4000\cdot0,3=1200N\)
b)Trọng lượng người đó: \(P=10m=10\cdot65=650N\)
Áp suất của máy giặt đặt trên mặt sàn:
\(p'=\dfrac{P}{S'}=\dfrac{650}{160\cdot10^{-4}}=40625N/m^2\)
Vậy \(p< < < p'\).

TL:
Tìm 1 cạnh của hình vuông: 280 : 4 = 70 ( ................ mik ko biết đơn vị là gì hết bạn ơi ! )
Diện tích hình vuông đó là: 70 x 70 = 4900 ( ..........2 )
Đáp số: 4900 .....2
Chúc bạn học tốt!
k mik nha!

1.A
2.A
3.B
4.C
5.B
6.C
7.A
8.A
9.B
10.A
11.B
12.A
13.C
14.B
15.B
16.A
17.A
18.A
19.A
20.C

Một gen có 2400 nucleotit ⇒ N = 2400 Nu
⇒ Số chu kì xoắn là:
C = N : 20 = 2400 : 20 = 120 (chu kì)

Bài 1:
\(a,A=6\sqrt{2}-6\sqrt{2}+2\sqrt{5}=2\sqrt{5}\\ b,B=\dfrac{\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}+\dfrac{\sqrt{2}\left(\sqrt{2}-1\right)}{\sqrt{2}-1}=\sqrt{3}+\sqrt{2}\\ c,=2\sqrt{3}-6\sqrt{3}+15\sqrt{3}-4\sqrt{3}=7\sqrt{3}\\ d,=1+6\sqrt{3}-\sqrt{3}-1=5\sqrt{3}\\ e,=4\sqrt{2}+\sqrt{2}-6\sqrt{2}+3\sqrt{2}=2\sqrt{2}\)
Bài 2:
\(a,ĐK:x\ge\dfrac{3}{2}\\ PT\Leftrightarrow\sqrt{2x-3}=5\Leftrightarrow2x-3=25\Leftrightarrow x=14\\ b,PT\Leftrightarrow x^2=\sqrt{\dfrac{98}{2}}=\sqrt{49}=7\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{7}\\x=-\sqrt{7}\end{matrix}\right.\\ c,ĐK:x\ge3\\ PT\Leftrightarrow\sqrt{x-3}\left(\sqrt{x+3}+1\right)=0\\ \Leftrightarrow\sqrt{x-3}=0\left(\sqrt{x+3}+1>0\right)\\ \Leftrightarrow x=3\\ d,ĐK:x\ge1\\ PT\Leftrightarrow2\sqrt{x-1}-\sqrt{x-1}+3\sqrt{x-1}=4\\ \Leftrightarrow\sqrt{x-1}=1\Leftrightarrow x=2\left(tm\right)\\ e,PT\Leftrightarrow2x-1=16\Leftrightarrow x=\dfrac{17}{2}\\ f,PT\Leftrightarrow\left|2x-1\right|=\sqrt{3}-1\Leftrightarrow\left[{}\begin{matrix}2x-1=\sqrt{3}-1\\2x-1=1-\sqrt{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{3}}{2}\\x=\dfrac{2-\sqrt{3}}{2}\end{matrix}\right.\)
Bài 3:
\(a,Q=\dfrac{1+5}{3-1}=3\\ b,P=\dfrac{x+\sqrt{x}-6+x-2\sqrt{x}-3-x+4\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ P=\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}}{\sqrt{x}-3}\\ c,M=\dfrac{\sqrt{x}}{\sqrt{x}-3}\cdot\dfrac{3-\sqrt{x}}{\sqrt{x}+5}=\dfrac{-\sqrt{x}}{\sqrt{x}+5}\)
Vì \(-\sqrt{x}\le0;\sqrt{x}+5>0\) nên \(M< 0\)
Do đó \(\left|M\right|>\dfrac{1}{2}\Leftrightarrow M< -\dfrac{1}{2}\Leftrightarrow-\dfrac{\sqrt{x}}{\sqrt{x}+5}+\dfrac{1}{2}< 0\)
\(\Leftrightarrow\dfrac{2\sqrt{x}-\sqrt{x}-5}{2\left(\sqrt{x}+5\right)}< 0\Leftrightarrow\sqrt{x}-5< 0\left(\sqrt{x}+5>0\right)\\ \Leftrightarrow0\le x< 25\)
Bài 4:
\(a,A=\dfrac{16+2\cdot4+5}{4-3}=29\\ b,B=\dfrac{2\sqrt{x}-9-x+9+2x-3\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ B=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\\ c,P=\dfrac{x+2\sqrt{x}+5}{\sqrt{x}-3}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}=\dfrac{x+2\sqrt{x}+5}{\sqrt{x}+1}\\ P=\dfrac{\left(\sqrt{x}+1\right)^2+4}{\sqrt{x}+1}=\sqrt{x}+1+\dfrac{4}{\sqrt{x}+1}\\ P\ge2\sqrt{\left(\sqrt{x}+1\right)\cdot\dfrac{4}{\sqrt{x}+1}}=2\sqrt{4}=4\\ P_{min}=4\Leftrightarrow\left(\sqrt{x}+1\right)^2=4\Leftrightarrow\sqrt{x}+1=2\Leftrightarrow x=1\left(tm\right)\)

 giúp mình với, mk cần gấp ạ, cảm ơn mn rất nhìu !
giúp mình với, mk cần gấp ạ, cảm ơn mn rất nhìu ! ai giúp mình phần 1 với ạ
ai giúp mình phần 1 với ạ 








\(\Leftrightarrow\sqrt{\left(x-2\right)^2}=7\)
\(\Leftrightarrow\left|x-2\right|=7\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=7\\x-2=-7\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=9\\x=-5\end{matrix}\right.\)
Ta có: \(\sqrt{x^2-4x+4}-5=2\)
\(\Leftrightarrow\left|x-2\right|=7\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=7\\x-2=-7\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=9\\x=-5\end{matrix}\right.\)