Tim x a)2x^2+50x=0 b)2x^3-50x=0 c)x4-8x=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 9 2016
a) \(\left(2x-1\right)^2-25=0\)
\(\left(2x-1\right)^2=0+25=25\)
\(\left(2x-1\right)^2=5^2=\left(-5\right)^2\)
\(\Rightarrow\left[\begin{array}{nghiempt}2x-1=5\\2x-1=-5\end{array}\right.\Rightarrow\left[\begin{array}{nghiempt}2x=6\\2x=-4\end{array}\right.\Rightarrow\left[\begin{array}{nghiempt}x=3\\x=-2\end{array}\right.\)
b) \(8x^3-50x=0\)
\(2x\left(4x^2-25\right)=0\)
\(\Rightarrow\left[\begin{array}{nghiempt}2x=0\\4x^2-25=0\end{array}\right.\Rightarrow\left[\begin{array}{nghiempt}x=0\\4x^2=25\Rightarrow x^2=\frac{25}{4}\Rightarrow\left[\begin{array}{nghiempt}x=\frac{5}{2}\\x=-\frac{5}{2}\end{array}\right.\end{array}\right.\)
27 tháng 5 2018
a) 2x(x - 3) + 5(x - 3) = 0 ⇔ (x - 3)(2x + 5) = 0 ⇔ x - 3 = 0 hoặc 2x + 5 = 0
1) x - 3 = 0 ⇔ x = 3
2) 2x + 5 = 0 ⇔ 2x = -5 ⇔ x = -2,5
Vậy tập nghiệm của phương trình là S = {3;-2,5}
b) (x2 - 4) + (x - 2)(3 - 2x) = 0 ⇔ (x - 2)(x + 2) + (x - 2)(3 - 2x) = 0
⇔ (x - 2)(x + 2 + 3 - 2x) = 0 ⇔ (x - 2)(-x + 5) = 0 ⇔ x - 2 = 0 hoặc -x + 5 = 0
1) x - 2 = 0 ⇔ x = 2
2) -x + 5 = 0 ⇔ x = 5
Vậy tập nghiệm của phương trình là S = {2;5}
c) x3 – 3x2 + 3x – 1 = 0 ⇔ (x – 1)3 = 0 ⇔ x = 1.
Vậy tập nghiệm của phương trình là x = 1
d) x(2x - 7) - 4x + 14 = 0 ⇔ x(2x - 7) - 2(2x - 7) = 0
⇔ (x - 2)(2x - 7) = 0 ⇔ x - 2 = 0 hoặc 2x - 7 = 0
1) x - 2 = 0 ⇔ x = 2
2) 2x - 7 = 0 ⇔ 2x = 7 ⇔ x = 72
Vậy tập nghiệm của phương trình là S = {2;72}
e) (2x – 5)2 – (x + 2)2 = 0 ⇔ (2x - 5 - x - 2)(2x - 5 + x + 2) = 0
⇔ (x - 7)(3x - 3) = 0 ⇔ x - 7 = 0 hoặc 3x - 3 = 0
1) x - 7 = 0 ⇔ x = 7
2) 3x - 3 = 0 ⇔ 3x = 3 ⇔ x = 1
Vậy tập nghiệm phương trình là: S= { 7; 1}
f) x2 – x – (3x - 3) = 0 ⇔ x2 – x – 3x + 3 = 0
⇔ x(x - 1) - 3(x - 1) = 0 ⇔ (x - 3)(x - 1) = 0
⇔ x = 3 hoặc x = 1
Vậy tập nghiệm của phương trình là S = {1;3}
VR
0
TT
2
29 tháng 10 2020
8x3 - 50x = 0
⇔ 2x( 4x2 - 25 ) = 0
⇔ 2x( 2x - 5 )( 2x + 5 ) = 0
⇔ 2x = 0 hoặc 2x - 5 = 0 hoặc 2x + 5 = 0
⇔ x = 0 hoặc x = ±5/2
( x + 3 )2 = 9( 2x - 1 )2
⇔ ( x + 3 )2 - 32( 2x - 1 )2 = 0
⇔ ( x + 3 )2 - [ 3( 2x - 1 ) ]2 = 0
⇔ ( x + 3 )2 - ( 6x - 3 )2 = 0
⇔ ( x + 3 - 6x + 3 )( x + 3 + 6x - 3 ) = 0
⇔ ( -5x + 6 ).7x = 0
⇔ -5x + 6 = 0 hoặc 7x = 0
⇔ x = 6/5 hoặc x = 0
29 tháng 10 2020
\(8x^3-50x=0\)
\(2x\left(4x^2-25\right)=0\)
\(\orbr{\begin{cases}2x=0\\4x^2-25=0\end{cases}}\)
\(\orbr{\begin{cases}x=0\\x^2=\frac{25}{4}\end{cases}}\)
\(\orbr{\begin{cases}x=0\\x=\pm\sqrt{\frac{25}{4}}\end{cases}}\)
\(\orbr{\begin{cases}x=0\\x=\pm\frac{5}{2}\end{cases}}\)
\(\left(x+3\right)^2=9\left(2x-1\right)^2\)
\(x^2+6x+9=9\left(4x^2-4x+1\right)\)
\(x^2+6x+9=36x^2-36x+9\)
\(0=36x^2-36x+9-x^2-6x-9\)
\(0=35x^2-42x\)
\(35x^2-42x=0\)
\(7x\left(5x-6\right)=0\)
\(\orbr{\begin{cases}7x=0\\5x-6=0\end{cases}}\)
\(\orbr{\begin{cases}x=0\\x=\frac{6}{5}\end{cases}}\)
TN
19 tháng 7 2016
a) (2x-1)^2-25=0
<=>(2x-1)2=52 hoặc (-5)2
<=>2x-1=5 hoặc -5
- Với 2x-1=5 <=>2x=6 <=>x=3
- Với 2x-1=-5 <=>2x=-4 <=>x=-2
b)8x^2-50x=0
<=>x(8x-50)=0
<=>x=0 hoặc 8x-50=0
- Với x=0
- Với 8x-50=0 <=>8x=50 <=>x=25/4
c)4x^2-25-(2x-5)(2x+7)=0
<=>4x2 - 25 - (4x2 + 14x - 10x - 35) = 0
<=>4x2 - 25 - 4x2 - 14x + 10x + 35 = 0
<=>-4x + 10 = 0
<=>-4x=-10
<=>x=5/2
d)x^3+27+(x+3)(x-9)=0
<=>x3+33+(x+3)(x-9)=0
<=>(x+3)(x2-3x+9)+(x+3)(x-9)=0
<=>(x+3)(x2-3x+9+x-9)=0
<=>(x+3)(x2-2x)=0
<=>(x+3)(x-2)x=0
<=>x+3=0 hoặc x-2=0 hoặc x=0
- VỚi x+3=0 <=>x=-3
- Với x-2=0 <=>x=2
- Với x=0
ML
2
27 tháng 10 2019
a) Ta có: \(\left(2x-1\right)^2-25=0\)
hay \(\left(2x-1\right)^2-5^2=0\)
\(\Rightarrow\left(2x-1-5\right)\left(2x-1+5\right)=0\)
\(\Rightarrow\left(2x-6\right)\left(2x+4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}2x-6=0\\2x+4=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}2x=6\\2x=-4\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\)
Vậy: \(x\in\left\{3;-2\right\}\)
b) Ta có: \(8x^2-50x=0\Rightarrow x\left(8x-50\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\8x-50=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\8x=50\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=\frac{50}{8}=\frac{25}{4}\end{matrix}\right.\)
Vậy: \(x\in\left\{0;\frac{25}{4}\right\}\)
c) Ta có: \(\left(x-2\right)\left(x^2+2x+7\right)+2\left(x^2-4\right)-5\left(x-2\right)=0\)
\(\Rightarrow\left(x-2\right)\left(x^2+2x+7\right)+2\left(x-2\right)\left(x+2\right)-5\left(x-2\right)=0\)
\(\Rightarrow\left(x-2\right)\left[\left(x^2+2x+7\right)+2\left(x+2\right)-5\right]=0\)
\(\Rightarrow\left(x-2\right)\left(x^2+2x+7+2x+4-5\right)=0\)
\(\Rightarrow\left(x-2\right)\left(x^2+4x+6\right)=0\)(1)
Ta có: \(x^2+4x+6=x^2+4x+4+2=\left(x+2\right)^2+2\)
mà \(\left(x+2\right)^2\ge0\forall x\)
nên \(\left(x+2\right)^2+2\ge2>0\forall x\)
nên \(x^2+4x+6=0\) là điều vô lý (2)
Từ (1) và (2) suy ra
\(x-2=0\Leftrightarrow x=2\)
Vậy: x=2
CB
2
17 tháng 7 2023
`@` `\text {Ans}`
`\downarrow`
`a,`
`(2x - 1)^2 - 25 = 0`
`<=> (2x - 1)^2 = 25`
`<=> (2x - 1)^2 = (+-5)^2`
`<=>`\(\left[{}\begin{matrix}2x-1=5\\2x-1=-5\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}2x=6\\2x=-4\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\)
Vậy, `S = {-2; 3}`
`b,`
`8x^3 - 50x = 0`
`<=> x(8x^2 - 50) = 0`
`<=>`\(\left[{}\begin{matrix}x=0\\8x^2-50=0\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}x=0\\8x^2=50\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}x=0\\x^2=\dfrac{25}{4}\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}x=0\\x=\pm\dfrac{5}{2}\end{matrix}\right.\)
Vậy, `S = {-5/2; 0; 5/2}.`
KV
17 tháng 7 2023
a) (2x - 1)² - 25 = 0
(2x - 1)² - 5² = 0
(2x - 1 - 5)(2x - 1 + 5) = 0
(2x - 6)(2x + 4) = 0
2x - 6 = 0 hoặc 2x + 4 = 0
*) 2x - 6 = 0
2x = 6
x = 3
*) 2x + 4 = 0
2x = -4
x = -2
Vậy x = -2; x = 3
b) 8x³ - 50x = 0
2x(4x² - 25) = 0
2x[(2x)² - 5²] = 0
2x(2x - 5)(2x + 5) = 0
2x = 0 hoặc 2x - 5 = 0 hoặc 2x + 5 = 0
*) 2x = 0
x = 0
*) 2x - 5 = 0
2x = 5
x = 5/2
*) 2x + 5 = 0
2x = -5
x = -5/2
Vậy x = -5/2; x = 0; x = 5/2
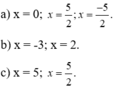
a)\(2x^2+50x=0\)
\(\Rightarrow x\left(2x+50\right)=0\)
\(\Rightarrow x=0\) hay \(2x+50=0\)
\(\Rightarrow2x=-50\)
\(\Rightarrow x=-25\)
b) \(2x^3-50x=0\)
\(\Rightarrow x\left(2x^2-50\right)=0\)
\(\Rightarrow x=0\) hay \(2x^2-50=0\)
\(2x^2=50\)
\(x^2=25\)
\(\Rightarrow x=5\) hay \(x=-5\)