x/3=y/4 và x2+y2=25 làm bằng hai cách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: (C1): x2+ y2 – 4 = 0 có tâm O (0; 0) và bán kính R= 2;
Dường tròn (C2): (x-3)2+ (y-4) 2= 25 có tâm I( 3;4) và R= 5 nên OI= 5
Ta thấy: 5-2 < OI< 5+ 2
nên chúng cắt nhau.
Chọn B.

\(a,y_2=kx_2\Rightarrow-2=5k\Rightarrow k=-\dfrac{2}{5}\) (k là hệ số tỉ lệ)
\(\Rightarrow y_1=-\dfrac{2}{5}x_1=-3\Rightarrow x_1=\dfrac{15}{2}\)
\(b,y_1=kx_1\Rightarrow k=\dfrac{3}{2}\\ \Rightarrow y_2=\dfrac{3}{2}x_2\\ \Rightarrow x_2+\dfrac{3}{2}x_2=10\\ \Rightarrow\dfrac{5}{2}x_2=10\Rightarrow x_2=4\\ \Rightarrow y_2=\dfrac{3}{2}\cdot4=6\)

Đoạn từ sau chữ "Biết" thiếu dấu liên kết giữa $x_1,y_1,x_2,y_2$. Bạn cần viết lại đề rõ hơn.

Theo t/c của dãy tỉ số bằng nhau ta có:
x/3=y/4=(x^2+y^2)/(3^2+4^2)=1
=>x=1.3=3
=>y=1.4=4
Mình viết bằng đt nên hơi khó hiểu thông cảm nhé
Đặt \(\dfrac{x}{3}=\dfrac{y}{4}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3k\\y=4k\end{matrix}\right.\)
Ta có: \(x^2+y^2=25\)
\(\Leftrightarrow k^2=1\)
Trường hợp 1: k=1
\(\Leftrightarrow\left\{{}\begin{matrix}x=3k=3\\y=4k=4\end{matrix}\right.\)
Trường hợp 2: k=-1
\(\Leftrightarrow\left\{{}\begin{matrix}x=3k=-3\\y=4k=-4\end{matrix}\right.\)

Vì \(x\) và \(y\) là hai đại tượng tỉ lệ nghịch nên \(xy=a\left(a\ne0\right)\)
Thay các giá trị tương ứng của \(x\) và \(y\) ta được :
\(x_1.y_1=x_2.y_2\)
\(\Rightarrow\dfrac{y_1}{x_2}=\dfrac{y_2}{x_1}\)
\(\Rightarrow\dfrac{y_1}{3}=\dfrac{y_2}{4}\)
- Áp dụng t/c dãy tỉ số bằng nhau, ta có :
\(\dfrac{y_1}{3}=\dfrac{y_2}{4}=\dfrac{y_1+y_2}{3+4}=\dfrac{14}{7}=2\)
\(\Rightarrow y_2=2.4=8\)

x2 + 4x – 2xy – 4y + y2 = (x2-2xy+ y2) + (4x – 4y) → bạn Việt dùng phương pháp nhóm hạng tử
= (x - y)2 + 4(x – y) → bạn Việt dùng phương pháp dùng hằng đẳng thức và đặt nhân tử chung
= (x – y)(x – y + 4) → bạn Việt dùng phương pháp đặt nhân tử chung

Vì x và y là hai đại lượng tỉ lệ nghịch nên x 1 y 1 = x 2 y 2 m à x 1 = 4 ; x 2 = 3 v à y 1 + y 2 = 14
Do đó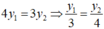
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
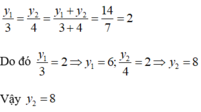
Chọn đáp án D

Với x và y là hai đại lượng tỉ lệ nghịch nên x 1 y 1 = x 2 y 2 mà x 1 = 4 , x 2 = 3 và y 1 + y 2 = 14
Do đó: 4 y 1 = 3 y 2 ⇒ y 1 3 = y 2 4
Áp dụng tính chất của dãy tỉ số bằng nhau ta được:
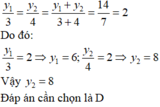
\(\frac{x}{3}\)=\(\frac{y}{4}\)=\(\frac{x^2}{9}\)=\(\frac{y^2}{16}\)=\(\frac{x^2+y^2}{9+16}\)=\(\frac{25}{25}\)=1
=> \(\hept{\begin{cases}x=3\\y=4\end{cases}}\)