Hộ mình bài 7A 7B vs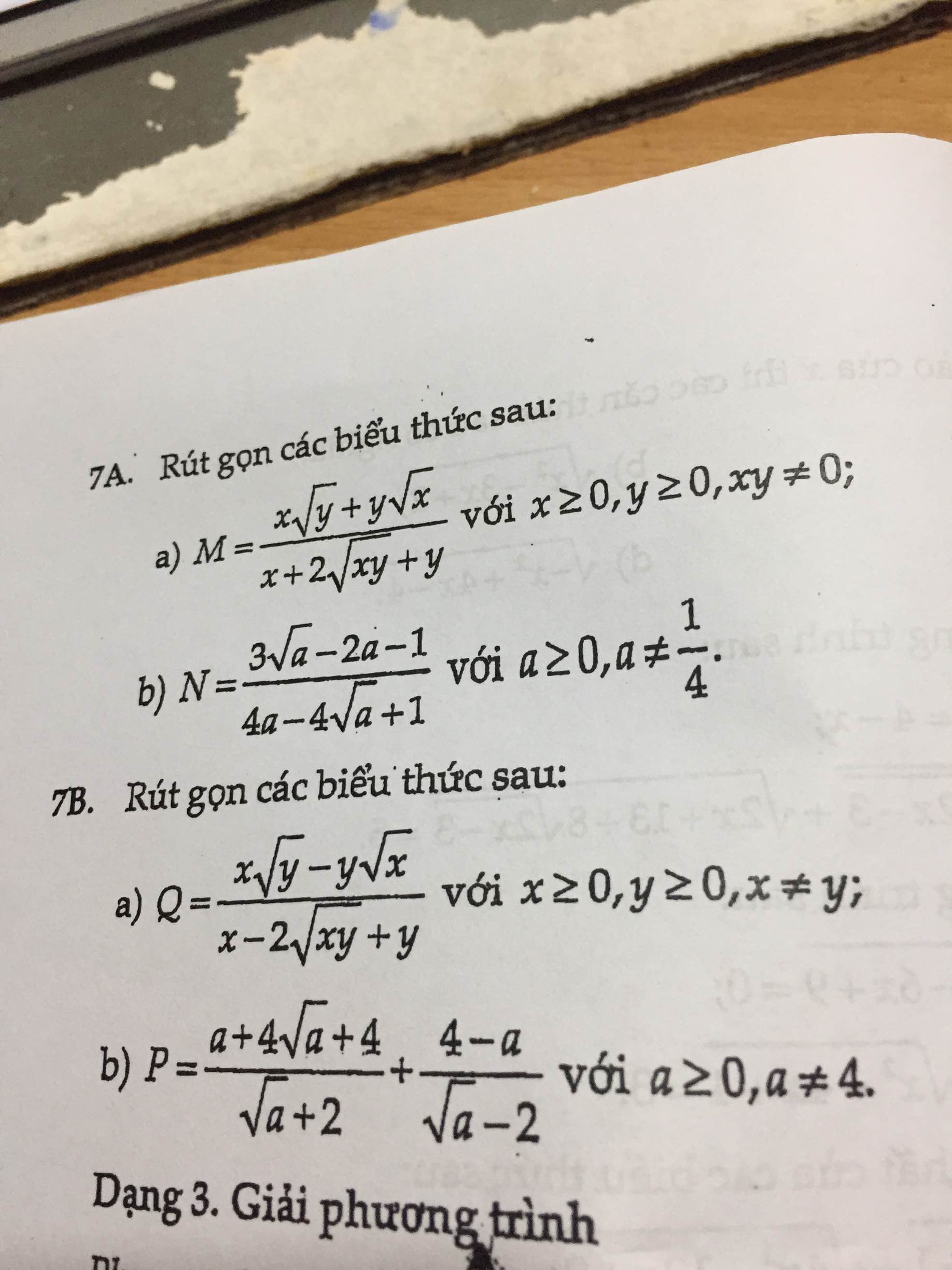
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số học sinh lớp 7a , 7b lần lượt là a ; b \(\left(a;b\inℕ^∗\right)\)
Theo bài ra ta có :
\(\frac{a}{6}=\frac{b}{7}\)
\(\Rightarrow\frac{a}{6}=\frac{2a}{12}=\frac{b}{7}\)và \(2a-b=25\)
ADTCDTSBN , ta có :
\(\frac{a}{6}=\frac{2a}{12}=\frac{b}{7}=\frac{2a-b}{12-7}=\frac{25}{5}=5\)
\(\Rightarrow\hept{\begin{cases}\frac{a}{6}=5\\\frac{b}{7}=5\end{cases}\Rightarrow\hept{\begin{cases}a=5.6=30\\b=5.7=35\end{cases}}}\)
Vậy ...

Số hs của 2 lớp là
35 + 40 = 75(hs)
Mỗi hs góp số tiền là:
1875000 : 75 = 25000(đồng)
Lớp 7A góp số tiền là:
25000 . 35 = 875000(đồng)
Lớp 7B góp số tiền là:
25000 . 40 = 1000000(đồng)
Đ/s: .............................

\(\text{Gọi x;y;z lần lượt là số tiền lớp 7A,7B,7C}\)
(đk:x;y;z\(\in\)N*,đơn vị:triệu đồng)
\(\text{Ta có:}\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{z}{6}\text{ và }x+y+z=30\)
\(\text{Áp dụng tính chất dãy tỉ số bằng nhau:}\)
\(\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{z}{6}=\dfrac{x+y+z}{4+5+6}=\dfrac{30}{15}=2\)
\(\Rightarrow x=2.4=8\text{(triệu đồng)}\)
\(y=2.5=10\text{(triệu đồng)}\)
\(z=2.6=12\text{(triệu đồng)}\)
\(\text{Vậy số tiền lớp 7A là:8 triệu đồng}\)
\(\text{lớp 7B là:10 triệu đồng}\)
\(\text{ lớp 7C là:12 triệu đồng}\)

Bài 2:
b: Xét tứ giác ABEC có
M là trung điểm của AE
M là trung điểm của BC
Do đó: ABEC là hình bình hành
Suy ra: AB//EC
Bài 2:
a) Xét tam giác MAB và tam giác MEC có:
+ MA = ME (gt).
+ MB = MC (M là trung điểm của BC).
+ \(\widehat{AMB}\) \(= \widehat{EMC}\) (đối đỉnh).
\(\Rightarrow\) Tam giác MAB = Tam giác MEC (c - g - c).
b) Ta có: \(\widehat{BAM}\) \(= \widehat{CEM}\) (Tam giác MAB = Tam giác MEC).
Mà 2 góc này ở vị trí so le trong.
\(\Rightarrow\) AB // EC (dhnb).

Gọi số quyển sách của mỗi lớp 7A, 7B, 7C lần lượt là a, b, c (a, b, c ∈ N*)
Theo giả thiết, ta có:
a+b+c=450; \(\frac{a}{6}=\frac{b}{5}=\frac{c}{4}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{6}=\frac{b}{5}=\frac{c}{4}=\frac{a+b+c}{6+5+4}=\frac{450}{15}=30\)
Do đó:
a=6.30=180 (quyển)
b=5.30=150 (quyển)
c=4.30=120 (quyển)
Vậy số quyển sách của mỗi lớp 7A, 7B, 7C quyên góp lần lượt là 180; 150 và 120 (quyển)

Gọi số cây trồng bốn lớp lần lượt theo thứ tự là: a;b;c
Áp dụng tính chất dãy tỉ số bằng nhau:
a/3= b/4 = c/5 = d/6 và b-a/4-3=5
a=5=> a=5.3=15
b=5=> b=5.4=20
c=5=> c=5.5=25
d=5=> d=5.6=30
vậy a=15; b=20; c=25; d=30
(em làm vậy thôi tuỳ trường mn bỏ hay thêm bước gì gì đó ạh)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{d}{6}=\dfrac{b-a}{4-3}=5\)
Do đó: a=15; b=20; c=25; d=30
7A
M=\(\dfrac{\sqrt{xy}\left(\sqrt{x}+\sqrt{y}\right)}{\left(\sqrt{x}+\sqrt{y}\right)^2}\) M= \(\dfrac{\sqrt{xy}}{\sqrt{x}+\sqrt{y}}\)
N = \(\dfrac{3\sqrt{a}-6a+4a-1}{\left(2\sqrt{a}-1\right)^2}\) N= \(\dfrac{-3\sqrt{a}\left(2\sqrt{a}-1\right)+\left(2\sqrt{a}-1\right).\left(2\sqrt{a}+1\right)}{\left(2\sqrt{a}-1\right)^2}\)
N= \(\dfrac{\left(2\sqrt{a}-1\right).\left(1-\sqrt{a}\right)}{\left(2\sqrt{a}-1\right)^2}\) N= \(\dfrac{1-\sqrt{a}}{2\sqrt{a}-1}\)
7B
Q= \(\dfrac{\sqrt{xy}\left(\sqrt{x}-\sqrt{y}\right)}{\left(\sqrt{x}-\sqrt{y}\right)^2}\) Q= \(\dfrac{\sqrt{xy}}{\sqrt{x}-\sqrt{y}}\)
P= \(\dfrac{\left(\sqrt{a}+2\right)^2}{\sqrt{a}+2}-\dfrac{\left(\sqrt{a}-2\right).\left(\sqrt{a}+2\right)}{\sqrt{a}-2}\)
P= \(\sqrt{a}+2-\sqrt{a}-2\) ; P = 0