Tìm các số tự nhiên a , b biết : \(3^a+3^b=108\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NK
1
25 tháng 7 2021
3^a +3^b = 108
=> 3^(a - 3) + 3^(b - 3) = 4 = 3^1 + 3^0 = 3^0 + 3^1
Th1 a - 3 = 1 và b - 3 = 0
=> a = 4 và b = 3
Th2 a - 3 = 0 và b - 4 = 0
=> a = 3 và b = 4
vậy (a ; b) là (3 ; 4) ; (4 ; 3)
16 tháng 8 2018
a. 2x - 138 = 23 . 32
2x = 72 + 138
x = 210 : 2
x = 105
b. 213 - (x - 6) = 1339 : 13
213 - (x - 6) = 103
x - 6 = 213 - 103
x = 110 + 6
x = 116
16 tháng 8 2018
2.x - 138 = 23 . 32
2.x - 138 = 8 . 9
2.x - 138 = 72
2.x = 72 + 138
2.x = 210
x = 105
b) 231 - (x - 6) = 1339 : 13
231 - x + 6 = 103
231 - x = 103 - 6
231 - x = 97
x = 231 - 97
x = 134
HD
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
11 tháng 11 2023
Vì 9040 chia cho 1 số ta được thương là 472 nên
Số đó là: 9040 : 472 = \(\dfrac{1130}{59}\) (không phải là số tự nhiên)
Nên không có số nào thỏa mãn đề bài.
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
11 tháng 11 2023
2, ƯCLN(a; b) = 9; a + b = 108
Vì ƯCLN(a; b) = 9 ⇒ a =9.d; b = 9.k (d; k) = 1; d; k \(\in\) N*
Theo bài ra ta có: 9d + 9k = 108
9.(d + k) = 108
d + k = 108 : 9
d + k = 12
(d; k) = (1; 11); (2; 10); (3; 9); (4; 8); (5; 7); (6; 6); (7; 5); (8; 4); (9; 3); (10; 2); (11; 1)
Vì (d; k) = (1; 11); (5; 7); (7; 5); (11; 1)
(a; b) = (9; 99); (45; 63); (63; 45); (99; 9)
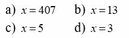
\(3^a+3^b=108\\ \Leftrightarrow3^{a-3}+3^{b-3}=4=3^1+3^0=3^0+3^1\)
Trường hợp 1:\(\left\{{}\begin{matrix}a-3=1\\b-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=4\\b=3\end{matrix}\right.\)
Trường hợp 2:\(\left\{{}\begin{matrix}a-3=0\\b-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=4\end{matrix}\right.\)
Vậy a = 3:b = 4 hoặc a = 4;b = 3
Giả sử a>=b
\(3^b(3^{a-b}+1)=3^3.4\)
Vì 3^b chỉ có thể có ước nguyên tố duy nhất là 3
3^(a-b)+1 không chia hết cho 3
nên b=3; 3^(a-b)+1=4
<=> b=3;a=4
Vậy a=4 b=3 hoặc a=3 b=4