Cho tam giác ABC vuông tại A, đường cao AH.
CMR: AB2= BH.BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
BT
2
Những câu hỏi liên quan
24 tháng 3 2023
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b: ΔABC đồng dạng với ΔHBA
=>BA/BH=BC/BA
=>BA^2=BH*BC
BH=3^2/5=1,8cm
c: BE là phân giác
=>AE/AB=HE/BH
=>AE/5=HE/3=(AE+HE)/(5+3)=0,3
=>AE=1,5cm và HE=0,9cm
17 tháng 4 2022
xét tam giác AHB và tam giác CAB có:
góc H = góc A = 90 độ
góc B chung
=> tam giác AHB ~ tam giác CAB
=> \(\dfrac{AB}{BC}\)=\(\dfrac{BH}{AB}\)
=> AB2= BH.BC
20 tháng 3 2023
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
=>BA/BH=BC/BA
=>BA^2=BH*BC
b: Xét ΔCDE vuông tại D và ΔCAB vuông tại A có
góc C chung
=>ΔCDE đồng dạng với ΔCAB
=>CD/CA=CE/CB
=>CD*CB=CA*CE
30 tháng 4 2023
a: \(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
BE là phân giác
=>AE/AB=CE/BC
=>AE/3=CE/5=16/8=2
=>AE=6cm; CE=10cm
b: Xet ΔHAB vuông tại H và ΔHCA vuông tại H có
góc HAB=góc HCA
=>ΔHAB đồng dạng vơi ΔHCA
c: ΔABC vuông tại A
mà AH là đường cao
nên BA^2=BH*BC
26 tháng 3 2023
a: Xet ΔABC vuông tại A và ΔHBA vuôngtại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
=>BA/BH=BC/BA
=>BA^2=BH*BC
b: Xét ΔAEB và ΔIEC có
góc BAE=góc EIC
góc AEB=góc IEC
=>góc ABE=góc ICE=góc IBC
=>ΔIEC đồng dạng với ΔICB
=>IE/IC=IC/IB
=>IC^2=IE*IB
c: Xét ΔBNC có
BI vừa là phân giác, vừa là đường cao
=>ΔBNC cân tại B
=>I là trung điểm của NC
ΔNAC vuông tại A
mà I là trung điểm của NC
nên IA=IN=IC
=>IN^2=IE*IB
và IA=IM
nên IM^2=IE*IB
=>IM/IE=IB/IM
=>ΔIMB đồng dạng với ΔIEM
=>góc IMB=90 độ
=>ĐPCM
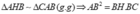
A B C H
Xét tam giác ABH và tam giác ABC có
góc AHB = góc BAC (= 90 độ)
góc BAH = góc C (cùng phụ góc B)
\(\Rightarrow\) tam giác HAB đồng dạng với tam giác ACB
\(\Rightarrow\frac{AB}{BC}=\frac{BH}{AB}\Rightarrow AB^2=BH\cdot BC\)
Xét tam giác ABH và tam giác CBA có:
góc B chung
góc AHB = góc CAB ( = 900)
=> 2 tam giác đồng dạng
\(\Rightarrow\frac{AB}{BC}=\frac{BH}{AB}\Rightarrow AB^2=BH.BC\)