Giải phương trình sin(x-50◘)=cos(x+120◘)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KM
1
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 11 2021
Với \(cosx=0\) ko phải nghiệm
Với \(cosx\ne0\) chia 2 vế cho \(cos^2x\)
\(\Rightarrow tan^2x-4\sqrt{3}tanx+1=-2\left(1+tan^2x\right)\)
\(\Leftrightarrow3tan^2x-4\sqrt{3}tanx+3=0\)
\(\Rightarrow\left[{}\begin{matrix}tanx=\sqrt{3}\\tanx=\dfrac{\sqrt{3}}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k\pi\\x=\dfrac{\pi}{6}+k\pi\end{matrix}\right.\)
PT
1
CM
7 tháng 6 2018
sin x + cos x = 1 + sin x.cos x
⇔ sin x.cos x – sin x – cos x + 1 = 0
⇔ (sinx. cosx –sinx)- (cosx -1 ) =0
⇔ sinx. (cosx – 1) – (cosx -1) = 0
⇔ (sin x – 1)(cos x – 1) = 0
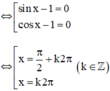
Vậy phương trình có tập nghiệm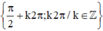 
AH
Akai Haruma
Giáo viên
18 tháng 7 2023
Lời giải:
$\sin 3x= \cos x= \sin (\frac{\pi}{2}-x)$
\(\Leftrightarrow \left[\begin{matrix} 3x=\frac{\pi}{2}-x+2k\pi\\ 3x=\pi -(\frac{\pi}{2}-x)+2k\pi\end{matrix}\right.(k\in\mathbb{Z})\)
\(\Leftrightarrow \left[\begin{matrix} x=\frac{1}{4}(2k+\frac{1}{2})\pi\\ x=\frac{1}{2}(2k+\frac{1}{2})\pi\end{matrix}\right. (k\in\mathbb{Z})\)
KH
0
BT
0
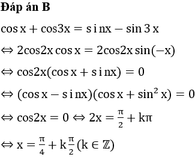
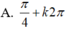
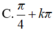
\(cos\left(x+120^0\right)=sin\left(x-50^0\right)\)
\(\Leftrightarrow cos\left(x+120^0\right)=cos\left(90^0-\left(x-50^0\right)\right)\)
\(\Leftrightarrow cos\left(x+120^0\right)=cos\left(140^0-x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x+120^0=140^0-x+k360^0\\x+120^0=x-140^0+k360^0\left(vn\right)\end{matrix}\right.\)
\(\Leftrightarrow2x=20^0+k360^0\)
\(\Leftrightarrow x=10^0+k180^0\)