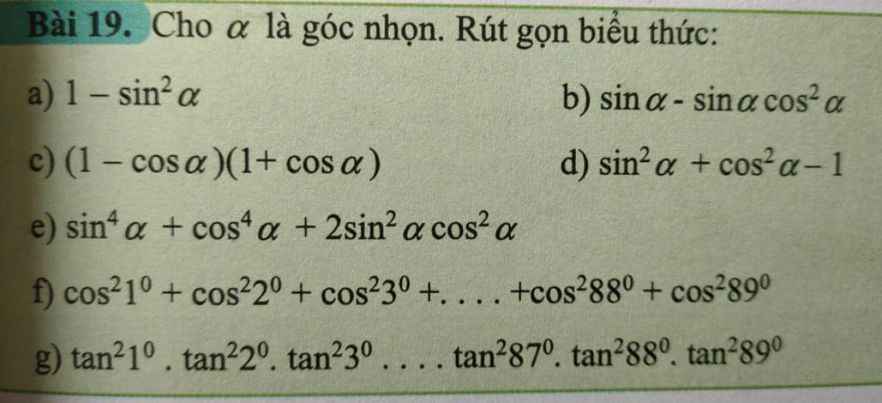Giải chi tiết giúp a b c
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KL
1
19 tháng 12 2021
a: Xét tứ giác ABDC có
N là trung điểm của BC
N là trung điểm của AD
Do đó: ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
VM
1
13 tháng 9 2016
4p(p-a)=2(a+b+c)[(b+c-a)/2]=(a+b+c)(c+b-a)(1)
b2+c2+2ab-a2=(a+b+c)(c+b-a)(2)
từ (1) và (2) suy ra b2+c2+2ab-a2=4p(p-a)
NH
3
11 tháng 8 2016
Theo đề bài, ta có:
0,2a=0,3b=0,4c và 2a+3b-5c=-1,8
\(\Rightarrow\frac{a}{0,2}=\frac{b}{0,3}=\frac{c}{0,4}\) và 2a+3b-5c=-1,8
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\frac{a}{0,2}=\frac{b}{0,3}=\frac{c}{0,4}=\frac{2a+3b-5c}{2.0,2+3.0,3-5.0,4}=\frac{\left(-1,8\right)}{\left(-0,7\right)}=\frac{18}{7}\)
- \(\frac{a}{0,2}=\frac{18}{7}.0,2=\frac{18}{35}\)
- \(\frac{b}{0,3}=\frac{18}{7}.0,3=\frac{27}{35}\)
- \(\frac{c}{0,4}=\frac{18}{7}.0,4=\frac{36}{35}\)
Vậy \(x=\frac{18}{35},y=\frac{27}{35},z=\frac{36}{35}\)
T mk nhé bạn ^...^ ^_^
11 tháng 8 2016
Ta có : \(0,2a=0,3b=\frac{a}{0,3}=\frac{b}{0,2}\)
\(0,3b=0,4c=\frac{b}{0,4}=\frac{c}{0,3}\)
Quy đòng : \(\frac{a}{0,3}=\frac{b}{0,2};\frac{b}{0,4}=\frac{c}{0,3};\frac{a}{0,12}=\frac{b}{0,08}=\frac{c}{0,06}\)
Áp dụng tính chất của dãy tỉ số bằng nhau , ta có :
Làm tiếp đi
10 tháng 3 2022
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
b: Ta có: ΔBAD=ΔBED
nên BA=BE
=>ΔBAE cân tại B
mà \(\widehat{ABE}=60^0\)
nên ΔABE đều
11 tháng 4 2022
\(f\left(0\right)=c=8\)
\(f\left(1\right)=a+b+c=a+b+8=9\Rightarrow a+b=1\) (1)
\(f\left(-1\right)=a-b+c=a-b+8=-11\Rightarrow a-b=-19\) (2)
-Từ (1) và (2) suy ra: \(a=-9;b=10\)
11 tháng 4 2022
f(0)=c=8f(0)=c=8
f(1)=a+b+c=a+b+8=9⇒a+b=1f(1)=a+b+c=a+b+8=9⇒a+b=1 (1)
f(−1)=a−b+c=a−b+8=−11⇒a−b=−19f(−1)=a−b+c=a−b+8=−11⇒a−b=−19 (2)
-Từ (1) và (2) suy ra: a=−9;b=10
N
23 tháng 6 2019
\(\left(a+b\right).\left(b+c\right).\left(c-a\right)+\left(b+c\right).\left(c+a\right).\left(a-b\right)+\left(c+a\right).\left(a+b\right).\left(b-c\right)\)
\(=\left(a+b\right).\left[\left(b+c\right).\left(c-a\right)+\left(c+a\right).\left(a-b\right)\right]+\left(c+a\right).\left(a+b\right).\left(b-c\right)\)
\(=\left(a+b\right).\left(ac-a^2+bc-ab+a^2-ab+ac-bc\right)+\left(c+a\right).\left(a+b\right).\left(b-c\right)\)
\(=-\left(a+b\right).2a.\left(b-c\right)+\left(c+a\right).\left(a+b\right).\left(b-c\right)\)
\(=\left(a+b\right).\left(b-c\right).\left(-2a+c+a\right)=\left(a+b\right).\left(b-c\right).\left(c-a\right)\)
N
23 tháng 6 2019
giai lai:
\(\left(b+c\right).\left[\left(a+b\right).\left(c-a\right)+\left(c+a\right).\left(a-b\right)\right]+\left(c+a\right).\left(a+b\right).\left(b-c\right)\)
\(=-\left(b+c\right).2a.\left(b-c\right)+\left(b-c\right).\left(ac+bc+a^2+ab\right)\)
\(=\left(b-c\right).\left(-2ab-2ac+ac+bc+a^2+ab\right)\)
\(=\left(b-c\right).\left(-ab-ac+bc+a^2\right)\)
\(=\left(b-c\right).\left(a+b\right).\left(a-c\right)\)
Lưu ý: \(1=sin^2a+cos^2a\)
Do đó:
a.
\(1-sin^2a=\left(sin^2a+cos^2a\right)-sin^2a=cos^2a\)
b.
\(sina-sina.cos^2a=sina\left(1-cos^2a\right)=sina\left(sin^2a+cos^2a-cos^2a\right)\)
\(=sina.sin^2a=sin^3a\)
c.
\(\left(1-cosa\right)\left(1+cosa\right)=1-cos^2a=sin^2a+cos^2a-cos^2a=sin^2a\)