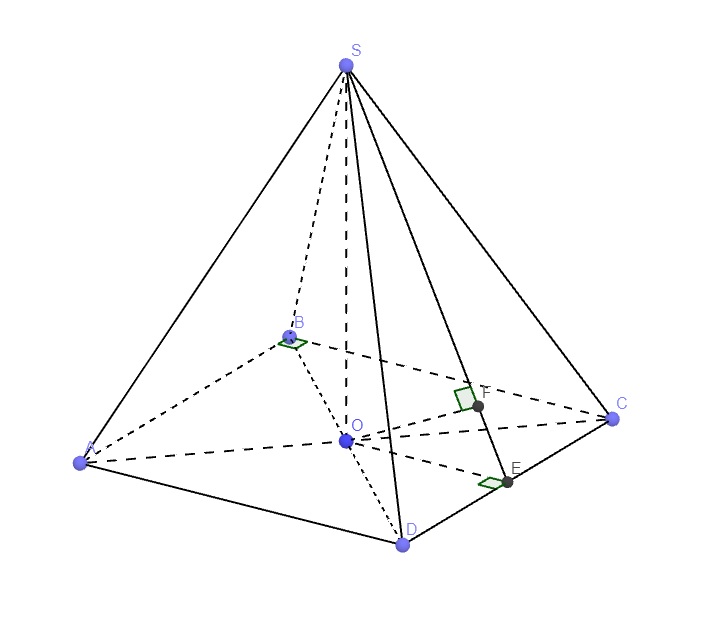
Cho hình chóp SABCD có đáy là hình chữ nhật tâm I, H là trung điểm của AI và SH vuông góc với đáy. Tính \(d_{\left(C,\left(SBD\right)\right)}\) biết \(AB=a,BC=a\sqrt{3}\) và tam giác SAC vuông tại S.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Do tam giác SAB đều và nằm trong mp vuông góc đáy \(\Rightarrow\) H là trung điểm AB
Gọi M là trung điểm AC\(\Rightarrow AM\perp AC\) (trung tuyến đồng thời là đường cao)
Gọi N là trung điểm AM \(\Rightarrow\) NH là đường trung bình tam giác AMH \(\Rightarrow NH||BM\Rightarrow NH\perp AC\)
\(\Rightarrow AC\perp\left(SNH\right)\)
Trong tam giác vuông SNH kẻ \(HK\perp SN\Rightarrow HK=d\left(H;\left(SAC\right)\right)\)
\(SH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
\(BM=\dfrac{a\sqrt{3}}{2}\Rightarrow NH=\dfrac{1}{2}BM=\dfrac{a\sqrt{3}}{4}\)
Hệ thức lượng:
\(\dfrac{1}{HK^2}=\dfrac{1}{SH^2}+\dfrac{1}{NH^2}=\dfrac{20}{3a^2}\Rightarrow NH=\dfrac{a\sqrt{15}}{10}\)

a.
\(\left\{{}\begin{matrix}SO\perp\left(ABCD\right)\Rightarrow SO\perp AC\\AC\perp BD\left(\text{hai đường chéo hình vuông}\right)\end{matrix}\right.\)
\(\Rightarrow AC\perp\left(SBD\right)\)
Mà \(AC\in\left(SAC\right)\Rightarrow\left(SAC\right)\perp\left(SBD\right)\)
b.
\(SO\perp\left(ABCD\right)\Rightarrow OC\) là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCO}\) là góc giữa SC và (ABCD)
\(OC=\dfrac{1}{2}AC=a\sqrt{2}\)
\(tan\widehat{SCO}=\dfrac{SO}{OC}=\sqrt{3}\Rightarrow\widehat{SCO}=60^0\)
c.
Gọi E là trung điểm CD, từ O kẻ \(OF\perp SE\)
OE là đường trung bình tam giác BCD \(\Rightarrow\left\{{}\begin{matrix}OE=\dfrac{1}{2}BC=a\\OE||BC\Rightarrow OE\perp CD\end{matrix}\right.\)
\(\Rightarrow CD\perp\left(SOE\right)\)\(\Rightarrow CD\perp OF\)
\(\Rightarrow OF\perp\left(SCD\right)\Rightarrow OF=d\left(O;\left(SCD\right)\right)\)
Do \(\left\{{}\begin{matrix}AO\cap\left(SCD\right)=C\\AC=2OC\end{matrix}\right.\) \(\Rightarrow d\left(AB;\left(SCD\right)\right)=d\left(A;\left(SCD\right)\right)=2d\left(O;\left(SCD\right)\right)=2OF\)
Hệ thức lượng: \(OF=\dfrac{OE.SO}{\sqrt{OE^2+SO^2}}=...\)

1: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
=>(SAC) vuông góc (SBD)