cho hình bình hành ABCD.Kẻ AH,CK vuông góc với BD.Chứng minh rằng: AHCK là hình thang
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 9 2021
a: Xét ΔADH vuông tại H và ΔCBK vuông tại K có
AD=CB
\(\widehat{D}=\widehat{B}\)
Do đó: ΔADH=ΔCBK
Suy ra: DH=BK
Ta có: DH+CH=DC
KB+AK=AB
mà DH=BK
và DC=AB
nên CH=AK
b: Xét tứ giác AHCK có
AK//CH
AK=CH
Do đó: AHCK là hình bình hành
CM
9 tháng 12 2018
Ta chứng minh AH//CK, AH = CK (DAHD = DCKB) Þ AHCK là hình bình hành (cặp cạnh đối song song và bằng nhau)
20 tháng 9 2021
a: Xét ΔADH vuông tại H và ΔCBK vuông tại K có
AD=CB
\(\widehat{ADH}=\widehat{CBK}\)
Do đó: ΔADH=ΔCBK
Suy ra: AH=CK
Xét tứ giác AHCK có
AH//CK
AH=CK
Do đó: AHCK là hình bình hành
22 tháng 7 2023
a: Xét ΔAHD vuông tại H và ΔCKB vuông tại K có
AD=CB
góc ADH=góc CBK
=>ΔAHD=ΔCKB
=>AH=CK
mà AH//CK
nên AHCK là hình bình hành
b: AHCK là hình bình hành
=>AC cắt HK tại trung điểm của mỗi đường
=>I là trung điểm của AC
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>I là trung điểm của BD
=>IB=ID
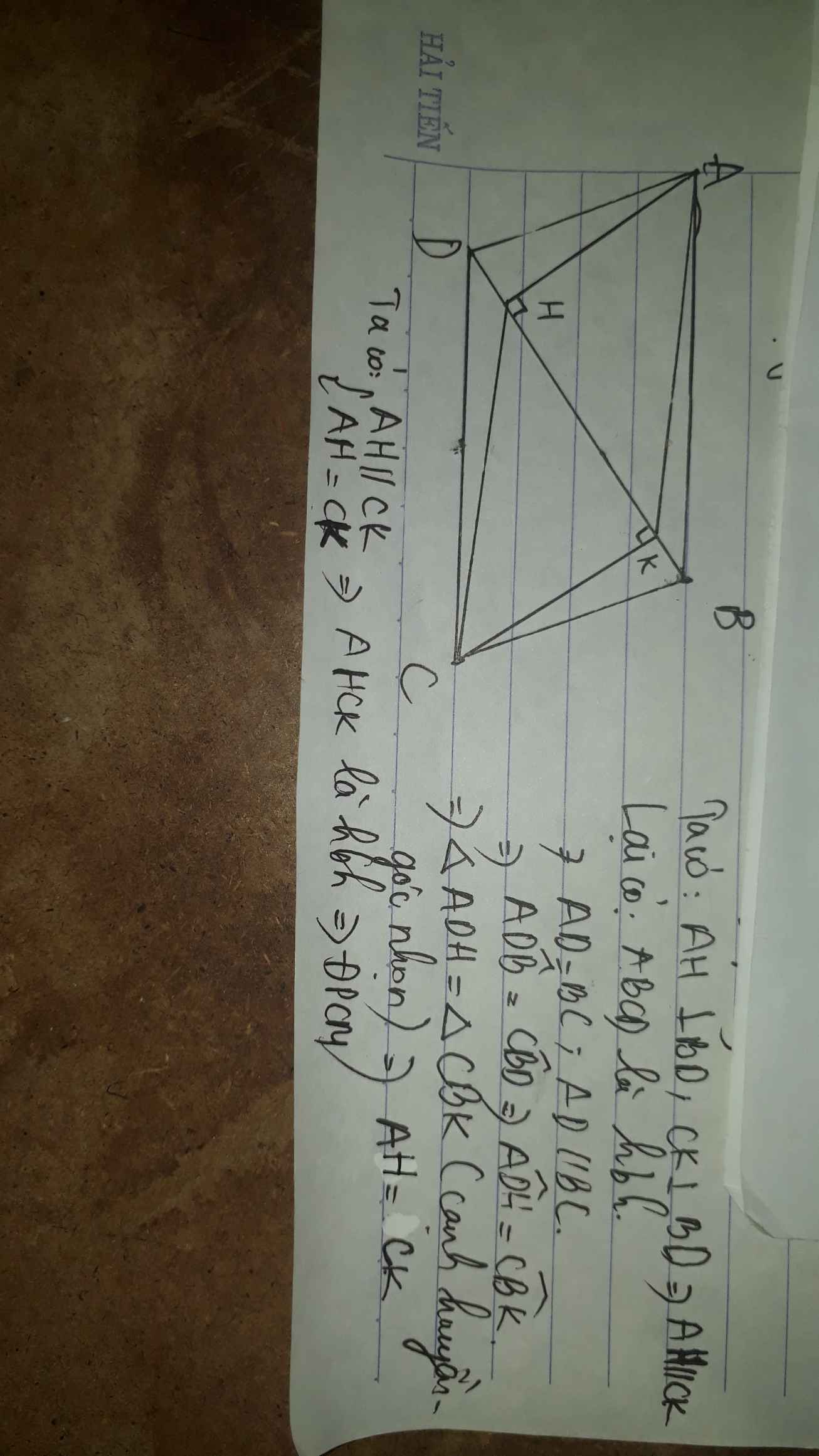
ta co
AH vuong goc BD ( gt)
CK vuong goc BD ( gt)
-> AH//CK
xet tu giac AHCK co AH//CK (Cmt)--> AHCK la hinh thang