Trong mặt phẳng toạ độ Oxy cho y=ax+b (a khác 0). Tìm các số nguyên a, b để đường thẳng đi qua M(4;3), cắt trục tung tại a' có tung độ là số nguyên dương, cắt trục hoành tại điểm có hoành độ là số nguyên dương.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 4 2020
14.
\(\overrightarrow{AB}=\left(-3;10\right)\) nên pt tham số của AB là: \(\left\{{}\begin{matrix}x=3-3t\\y=-4+10t\end{matrix}\right.\)
15.
Do d song song delta nên d nhận \(\left(2;-1\right)\) là 1 vtcp
Phương trình tham số d: \(\left\{{}\begin{matrix}x=2t\\y=-4-t\end{matrix}\right.\)
18.
d có vtcp là (2;3) nên d nhận (3;-2) là 1 vtpt
Phương trình d:
\(3\left(x+1\right)-2\left(y-0\right)=0\Leftrightarrow3x-2y+3=0\)
19.
\(\overrightarrow{AB}=\left(3;-4\right)\Rightarrow\) đường thẳng AB nhận (4;3) là 1 vtpt
Phương trình d:
\(4\left(x+2\right)+3\left(y-4\right)=0\Leftrightarrow4x+3y-4=0\)
9 tháng 2 2022
a: Theo đề, ta có:
\(\left\{{}\begin{matrix}a+b=5\\2a+b=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=2\end{matrix}\right.\)
b:
1: Thay x=-1 và y=3 vào (d), ta được:
\(2\cdot\left(-1\right)-a+1=3\)
=>-a-1=3
=>-a=4
hay a=-4
22 tháng 1 2021
Sửa đề: (d)//y=x+1
Để (d) song song với đường thẳng y=x+1 thì \(\left\{{}\begin{matrix}a=1\\b\ne1\end{matrix}\right.\)
hay (d): y=x+b
Vì (d) đi qua M(1;-2) nên Thay x=1 và y=-2 vào hàm số y=x+b, ta được:
\(b+1=-2\)
hay b=-3
Vậy: a=1 và b=-3
HQ
Hà Quang Minh
Giáo viên
30 tháng 9 2023
a) Khoảng cách từ điểm A đến đường thẳng \(\Delta \) là: \(d\left( {A,\Delta } \right) = \frac{{\left| {0 - 2 - 4} \right|}}{{\sqrt {{1^2} + {1^2}} }} = 3\sqrt 2 \).
b) Ta có: \(\overrightarrow {{n_a}} = \overrightarrow {{n_\Delta }} = \left( {1;1} \right)\). Phương trình đường thẳng a là:
\(1\left( {x + 1} \right) + 1\left( {y - 0} \right) = 0 \Leftrightarrow x + y + 1 = 0\)
c) Ta có: \(\overrightarrow {{u_a}} = \overrightarrow {{n_\Delta }} = \left( {1;1} \right)\).Từ đó suy ra \(\overrightarrow {{n_b}} = \left( {1; - 1} \right)\). Phương trình đường thẳng b là:
\(1\left( {x - 0} \right) - 1\left( {y - 3} \right) = 0 \Leftrightarrow x - y + 3 = 0\)
NM
Nguyễn Minh Quang
Giáo viên
11 tháng 5 2021
Vì đường thẳng song song với y =3x +1 nên
\(a=3\) Vậy đường thẳng có dạng \(y=3x+b\)
Do đường thẳng đi qua điểm M nên :
\(2=3\times-1+b\Leftrightarrow b=5\)
Vậy \(\hept{\begin{cases}a=3\\b=5\end{cases}}\)
2
19 tháng 5 2023
`a)`
`@ O(0;0), A(1;1), B(-1;1) in (P)`
`@ C(0;2), D(-2;0) in (d)`
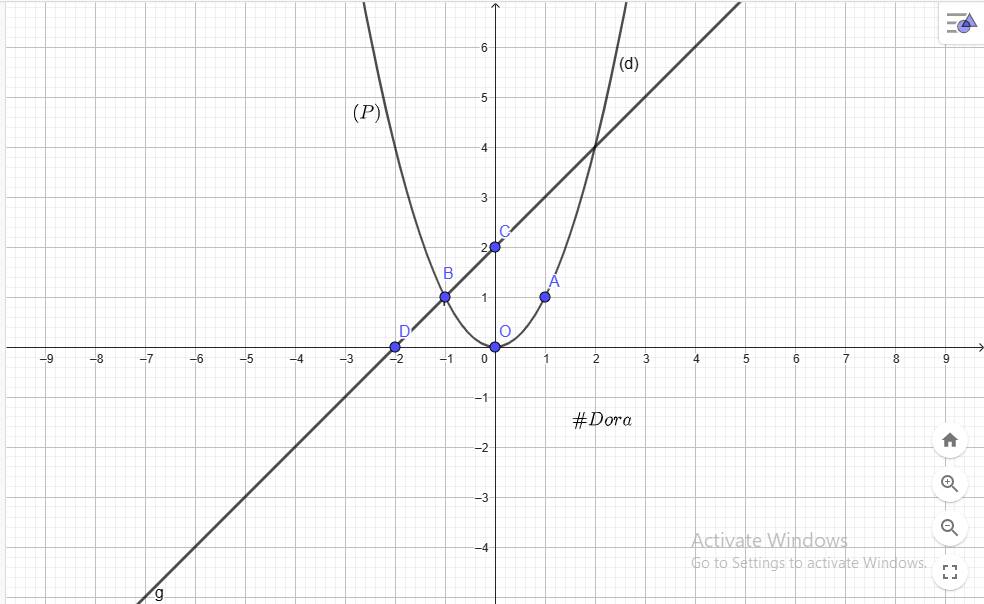
`b)` Ptr hoành độ của `(P)` và `(d)` là:
`x^2=x+2`
`<=>x^2-x-2=0`
Ptr có: `a-b+c=1+1-2=0`
`=>x_1=-1;x_2=-c/a=2`
`=>y_1=1;y_2=4`
`=>(-1;1), (2;4)` là giao điểm của `(P)` và `(d)`
`c)` Vì `(d') //// (d)=>a=1` và `b ne 2`
Thay `a=1;M(2;5)` vào `(d')` có:
`5=2+b<=>b=3` (t/m)
`=>` Ptr đường thẳng `(d'): y=x+3`
Do đường thẳng qua M nên: \(4a+b=3\Rightarrow b=3-4a\)
b dương \(\Rightarrow3-4a>0\Rightarrow a< \dfrac{3}{4}\) (1)
Pt đường thẳng: \(y=ax-4a+3\)
Giao điểm với trục hoành:
\(ax-4a+3=0\Rightarrow x=\dfrac{4a-3}{a}=4-\dfrac{3}{a}\)
Do hoành độ là số nguyên \(\Rightarrow3-\dfrac{3}{a}\in Z\)
\(\Leftrightarrow\dfrac{3}{a}\in Z\) \(\Rightarrow a=\left\{-3;-1;1;3\right\}\)
Kết hợp điều kiện (1) \(\Rightarrow a=\left\{-3;-1\right\}\)
\(\Rightarrow b=\left\{15;7\right\}\)
Vậy \(\left(a;b\right)=\left(-3;15\right);\left(-1;7\right)\)