làm giúp mình 4 bài này mình cần gấp...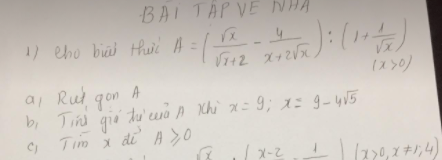
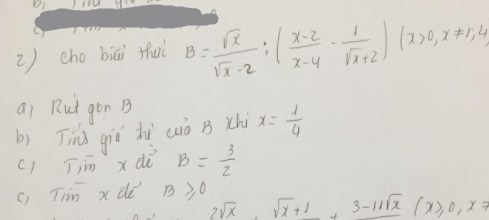
Đọc tiếp
làm giúp mình 4 bài này mình cần gấp ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 1 2022
Bài 2:
a: =>168x+20=6x-21
=>162x=-41
hay x=-41/162
b: \(\Leftrightarrow2\left(3x-8\right)=3\left(5-x\right)\)
=>6x-16=15-3x
=>9x=31
hay x=31/9
c: \(\Leftrightarrow4\left(x^2+8x-20\right)-\left(x+4\right)\left(x+10\right)=3\left(x^2+2x-8\right)\)
\(\Leftrightarrow4x^2+32x-80-x^2-14x-40-3x^2-6x+24=0\)
=>12x-96=0
hay x=8
PA
1
17 tháng 7 2021
1) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8(cm)
21 tháng 10 2021
Câu 9.
3/2.x -7/3 = -1/4
3/2.x= -1/4-(-7/3)
3/2.x= 25/12
x= 25/12 : 3/2 = 25/18
21 tháng 10 2021
Ix+4/5I-2/9=3/5
Ix+4/5I= 3/5 + 2/9
Ix+4/5I= 37/45
x+4/5= 37/45
-37/45
x= 37/45 - 4/5
-37/45 - 4/5
x = 1/45
-73/45
28 tháng 1 2023
a: Xét tứ giác MBQC có
N la trung điểm chung của MQ và BC
=>MBQC là hình bình hành
b: Xet tứ giácc AMQC có
AM//QC
AM=QC
góc MAC=90 độ
=>AMQC là hình chữ nhật
c: Xét ΔBAC có
N là trung điểm của CB
NK//AB
=>K là trung điểm của AC
Xét ΔCAB có
AN,BK,CM là các trung tuyến
nên ba đường này sẽ đồng quy
=>B,H,K thẳng hàng
5 tháng 12 2021
\(R_{tđ}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{24\cdot12}{24+12}=8\Omega\)
\(I=\dfrac{U}{R}=\dfrac{12}{8}=1,5A\)
\(P=\dfrac{U^2}{R}=\dfrac{12^2}{8}=18W\)
\(Q_{tỏa1}=A_1=U_1\cdot I_1\cdot t=12\cdot\dfrac{12}{24}\cdot1\cdot3600=21600J\)
\(Q_{tỏa2}=A_2=U_2\cdot I_2\cdot t=12\cdot\dfrac{12}{12}\cdot1\cdot3600=43200J\)
NL
0
NL
1
21 tháng 3 2022
a)
Gọi số mol Fe, Fe2O3 là a, b (mol)
=> 56a + 160b = 48,8 (1)
PTHH: 2Fe + 6H2SO4 --> Fe2(SO4)3 + 3SO2 + 6H2O
a-------------------->0,5a------>1,5a
Fe2O3 + 3H2SO4 --> Fe2(SO4)3 + 3H2O
b----------------------->b
=> \(0,5a+b=\dfrac{140}{400}=0,35\) (2)
(1)(2) => a = 0,3 (mol); b = 0,2 (mol)
=> \(\left\{{}\begin{matrix}\%m_{Fe}=\dfrac{0,3.56}{48,8}.100\%=34,426\%\\\%m_{Fe_2O_3}=\dfrac{0,2.160}{48,8}.100\%=65,574\%\end{matrix}\right.\)
b) nSO2 = 1,5a = 0,45 (mol)
nNaOH = 1.0,45 (mol)
Xét tỉ lệ: \(\dfrac{n_{NaOH}}{n_{SO_2}}=\dfrac{0,45}{0,45}=1\) => Tạo muối NaHSO3
PTHH: NaOH + SO2 --> NaHSO3
0,45-------------->0,45
=> \(C_{M\left(dd.NaHSO_3\right)}=\dfrac{0,45}{0,45}=1M\)
26 tháng 9 2021
\(a,=2\sqrt{2}\left(\sqrt{5}-1\right)\sqrt{4+\sqrt{\left(\sqrt{5}-1\right)^2}}\\ =2\sqrt{2}\left(\sqrt{5}-1\right)\sqrt{4+\sqrt{5}-1}\\ =2\left(\sqrt{5}-1\right)\sqrt{6-2\sqrt{5}}\\ =2\left(\sqrt{5}-1\right)\sqrt{\left(\sqrt{5}-1\right)^2}\\ =2\left(\sqrt{5}-1\right)^2=2\left(6-2\sqrt{5}\right)=12-4\sqrt{5}\\ b,=\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{8-2\sqrt{15}}\\ =\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}\\ =\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)^2\\ =\left(4+\sqrt{15}\right)\left(8-2\sqrt{15}\right)\\ =32-8\sqrt{15}+8\sqrt{15}-30=2\)
2) Ta có: \(B=\dfrac{\sqrt{x}}{\sqrt{x}-2}:\left(\dfrac{x-2}{x-4}-\dfrac{1}{\sqrt{x}+2}\right)\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-2}:\dfrac{x-2-\sqrt{x}+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-2}\cdot\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}{x-\sqrt{x}}\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\)