Tìm tất cả các giá trị thực của tham số \(a\) để tích phân \(\int\limits^{1+a}_1\dfrac{1}{x\left(x-5\right)\left(x-4\right)}dx\) tồn tại
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 11 2021
Khi gặp dạng này, ý tưởng là sẽ tìm 1 hàm u(x) sao cho:
\(\int\limits^b_a\left[f'\left(x\right)-u\left(x\right)\right]^2dx=0\) (1)
\(\Rightarrow f'\left(x\right)-u\left(x\right)=0\Rightarrow f'\left(x\right)=u\left(x\right)\)
Khai triển (1), đề cho sẵn \(\left[f'\left(x\right)\right]^2\) nên đại lượng \(2u\left(x\right).f'\left(x\right)\) và hàm \(u\left(x\right)\) sẽ được suy ra từ việc tích phân từng phần \(\int\limits f\left(x\right)dx\). Cụ thể:
Xét \(I=\dfrac{2}{3}=\int\limits^2_0f\left(x\right)dx\)
Đặt \(\left\{{}\begin{matrix}u=f\left(x\right)\\dv=dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'\left(x\right)dx\\v=x\end{matrix}\right.\)
\(\Rightarrow I=x.f\left(x\right)|^2_0-\int\limits^2_0xf'\left(x\right)dx=2-\int\limits^2_0xf'\left(x\right)dx\)
\(\Rightarrow\int\limits^2_0xf'\left(x\right)dx=2-\dfrac{2}{3}=\dfrac{4}{3}\) (2)
(Vậy đến đây hàm \(u\left(x\right)\) được xác định là dạng \(u\left(x\right)=k.x\)
Để tìm cụ thể giá trị k:
Từ (1) ta suy luận tiếp:
\(\int\limits^2_0\left[f'\left(x\right)-kx\right]^2dx=0\Leftrightarrow\int\limits^2_0\left[f'\left(x\right)\right]^2-2k\int\limits^2_0x.f'\left(x\right)dx+\int\limits^2_0k^2x^2dx=0\)
\(\Leftrightarrow\dfrac{2}{3}-2k.\dfrac{4}{3}+\dfrac{8}{3}k^2=0\) do \(\int\limits^2_0x^2dx=\dfrac{8}{3}\)
\(\Rightarrow k=\dfrac{1}{2}\)
\(\Rightarrow u\left(x\right)=\dfrac{1}{2}x\) coi như xong bài toán)
Do đó ta có:
\(\int\limits^2_0\left[f'\left(x\right)\right]^2-\int\limits^2_0xf'\left(x\right)+\dfrac{1}{4}\int\limits^2_0x^2dx=\dfrac{2}{3}-\dfrac{4}{3}+\dfrac{1}{4}.\dfrac{8}{3}=0\)
\(\Rightarrow\int\limits^2_0\left[f'\left(x\right)-\dfrac{1}{2}x\right]^2dx=0\)
\(\Rightarrow f'\left(x\right)-\dfrac{1}{2}x=0\)
\(\Rightarrow f'\left(x\right)=\dfrac{1}{2}x\Rightarrow f\left(x\right)=\dfrac{1}{4}x^2+C\)
Thay \(x=2\Rightarrow1=1+C\Rightarrow C=0\)
\(\Rightarrow f\left(x\right)=\dfrac{1}{4}x^2\)
LN
1 tháng 4 2017
a) =
=
b) =
=
=
c)=
d)=
=
e)=
=
g)Ta có f(x) = sin3xcos5x là hàm số lẻ.
Vì f(-x) = sin(-3x)cos(-5x) = -sin3xcos5x = f(-x) nên:
AH
Akai Haruma
Giáo viên
8 tháng 7 2017
a)
Ta có \(A=\int ^{\frac{\pi}{4}}_{0}\cos 2x\cos^2xdx=\frac{1}{4}\int ^{\frac{\pi}{4}}_{0}\cos 2x(\cos 2x+1)d(2x)\)
\(\Leftrightarrow A=\frac{1}{4}\int ^{\frac{\pi}{2}}_{0}\cos x(\cos x+1)dx=\frac{1}{4}\int ^{\frac{\pi}{2}}_{0}\cos xdx+\frac{1}{8}\int ^{\frac{\pi}{2}}_{0}(\cos 2x+1)dx\)
\(\Leftrightarrow A=\frac{1}{4}\left.\begin{matrix} \frac{\pi}{2}\\ 0\end{matrix}\right|\sin x+\frac{1}{16}\left.\begin{matrix} \frac{\pi}{2}\\ 0\end{matrix}\right|\sin 2x+\frac{1}{8}\left.\begin{matrix} \frac{\pi}{2}\\ 0\end{matrix}\right|x=\frac{1}{4}+\frac{\pi}{16}\)
b)
\(B=\int ^{1}_{\frac{1}{2}}\frac{e^x}{e^{2x}-1}dx=\frac{1}{2}\int ^{1}_{\frac{1}{2}}\left ( \frac{1}{e^x-1}-\frac{1}{e^x+1} \right )d(e^x)\)
\(\Leftrightarrow B=\frac{1}{2}\left.\begin{matrix} 1\\ \frac{1}{2}\end{matrix}\right|\left | \frac{e^x-1}{e^x+1} \right |\approx 0.317\)
AH
Akai Haruma
Giáo viên
8 tháng 7 2017
c)
Có \(C=\int ^{1}_{0}\frac{(x+2)\ln(x+1)}{(x+1)^2}d(x+1)\).
Đặt \(x+1=t\)
\(\Rightarrow C=\int ^{2}_{1}\frac{(t+1)\ln t}{t^2}dt=\int ^{2}_{1}\frac{\ln t}{t}dt+\int ^{2}_{1}\frac{\ln t}{t^2}dt\)
\(=\int ^{2}_{1}\ln td(\ln t)+\int ^{2}_{1}\frac{\ln t}{t^2}dt=\frac{\ln ^22}{2}+\int ^{2}_{1}\frac{\ln t}{t^2}dt\)
Đặt \(\left\{\begin{matrix} u=\ln t\\ dv=\frac{dt}{t^2}\end{matrix}\right.\Rightarrow \left\{\begin{matrix} du=\frac{dt}{t}\\ v=\frac{-1}{t}\end{matrix}\right.\Rightarrow \int ^{2}_{1}\frac{\ln t}{t^2}dt=\left.\begin{matrix} 2\\ 1\end{matrix}\right|-\frac{\ln t+1}{t}=\frac{1}{2}-\frac{\ln 2 }{2}\)
\(\Rightarrow C=\frac{1}{2}-\frac{\ln 2}{2}+\frac{\ln ^22}{2}\)
DL
20 tháng 2 2021
Câu nào mình biết thì mình làm nha.
1) Đổi thành \(\dfrac{y^4}{4}+y^3-2y\) rồi thế số.KQ là \(\dfrac{-3}{4}\)
2) Biến đổi thành \(\dfrac{t^2}{2}+2\sqrt{t}+\dfrac{1}{t}\) và thế số.KQ là \(\dfrac{35}{4}\)
3) Biến đổi thành 2sinx + cos(2x)/2 và thế số.KQ là 1
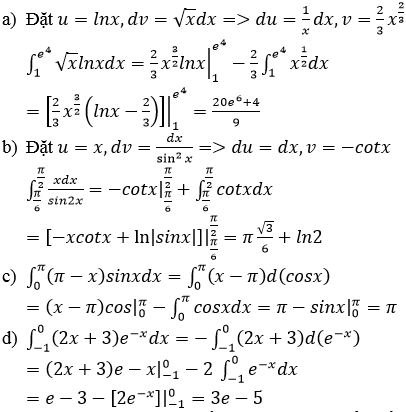
Tích phân đã cho tồn tại khi hàm \(\dfrac{1}{x\left(x-5\right)\left(x-4\right)}\) xác định với mọi x thuộc \(\left[1;1+a\right]\) với \(a>0\) hoặc \(\left[1+a;1\right]\) với \(a< 0\)
ĐKXĐ: \(x\ne\left\{0;4;5\right\}\) hay \(x\in\left(-\infty;0\right)\cup\left(0;4\right)\cup\left(4;5\right)\cup\left(5;+\infty\right)\)
Do 2 khoảng \(\left[1;1+a\right]\) và \(\left[1+a;1\right]\) đều chứa số 1 nằm trong \(\left(0;4\right)\)
\(\Rightarrow\)Bài toán thỏa mãn khi \(\left[{}\begin{matrix}\left[1;a+1\right]\subset\left(0;4\right)\\\left[1+a;1\right]\subset\left(0;4\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}1< 1+a< 4\\0< 1+a< 1\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}0< a< 3\\-1< a< 0\end{matrix}\right.\)