Cho a3 + b3 = 2 Chứng mình rằng : a + b \(\le\)2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(a^2+b^2-ab\ge\dfrac{1}{2}\left(a+b\right)^2-\dfrac{1}{4}\left(a+b\right)^2=\dfrac{1}{4}\left(a+b\right)^2\)
Lại có:
\(2=a^3+b^3=\left(a+b\right)\left(a^2+b^2-ab\right)\)
Mà \(a^2+b^2-ab>0\Rightarrow a+b>0\)
\(\Rightarrow2=\left(a+b\right)\left(a^2+b^2-ab\right)\ge\left(a+b\right).\dfrac{1}{4}\left(a+b\right)^2=\dfrac{1}{4}\left(a+b\right)^3\)
\(\Rightarrow\left(a+b\right)^3\le8\Rightarrow a+b\le2\)

1. b3+b= 3
(b3+b)=3
b.(3+1)=3
b. 4= 3
b=\(\dfrac{3}{4}\)
a3+a= 3 b3
(a3+a)=3
a.(3+1)=3
a. 4= 3
a=\(\dfrac{3}{4}\)
2

Câu 9:
\(a,\left(a+1\right)^2\ge4a\\ \Leftrightarrow a^2+2a+1\ge4a\\ \Leftrightarrow a^2-2a+1\ge0\\ \Leftrightarrow\left(a-1\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow a=1\)
\(b,\) Áp dụng BĐT cosi: \(\left(a+1\right)\left(b+1\right)\left(c+1\right)\ge2\sqrt{a}\cdot2\sqrt{b}\cdot2\sqrt{c}=8\sqrt{abc}=8\)
Dấu \("="\Leftrightarrow a=b=c=1\)
Câu 10:
\(a,\left(a+b\right)^2\le2\left(a^2+b^2\right)\\ \Leftrightarrow a^2+2ab+b^2\le2a^2+2b^2\\ \Leftrightarrow a^2-2ab+b^2\ge0\\ \Leftrightarrow\left(a-b\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow a=b\)
\(b,\Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac\le3a^2+3b^2+3c^2\\ \Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow a=b=c\)
Câu 13:
\(M=\left(a^2+ab+\dfrac{1}{4}b^2\right)-3\left(a+\dfrac{1}{2}b\right)+\dfrac{3}{4}b^2-\dfrac{3}{2}b+2021\\ M=\left[\left(a+\dfrac{1}{2}b\right)^2-2\cdot\dfrac{3}{2}\left(a+\dfrac{1}{2}b\right)+\dfrac{9}{4}\right]+\dfrac{3}{4}\left(b^2-2b+1\right)+2018\\ M=\left(a+\dfrac{1}{2}b-\dfrac{3}{2}\right)^2+\dfrac{3}{4}\left(b-1\right)^2+2018\ge2018\\ M_{min}=2018\Leftrightarrow\left\{{}\begin{matrix}a+\dfrac{1}{2}b=\dfrac{3}{2}\\b=1\end{matrix}\right.\Leftrightarrow a=b=1\)
Câu 6:
$2=(a+b)(a^2-ab+b^2)>0$
$\Rightarrow a+b>0$
$4(a^3+b^3)-N^3=4(a^3+b^3)-(a+b)^3$
$=3(a^3+b^3)-3ab(a+b)=(a+b)(a-b)^2\geq 0$
$\Rightarrow N^3\leq 4(a^3+b^3)=8$
$\Rightarrow N\leq 2$
Vậy $N_{\max}=2$

\(\Leftrightarrow a^3+b^3+c^3-3abc>=0\)
\(\Leftrightarrow\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc>=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ac\right)>=0\)
\(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2bc-2ac>=0\)(vì a+b+c>0)
\(\Leftrightarrow\left(a-b\right)^2+\left(a-c\right)^2+\left(b-c\right)^2>=0\)(luôn đúng)
\(a^3+b^3+c^3\ge3abc\\ \Leftrightarrow\left(a+b\right)^3-3ab\left(a+b\right)+c^3-3abc\ge0\\ \Leftrightarrow\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2\right)-3ab\left(a+b+c\right)\ge0\\ \Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)\ge0\)
Vì \(a,b,c>0\Leftrightarrow a+b+c>0\)
Lại có \(a^2+b^2+c^2-ab-bc-ca=\dfrac{1}{2}\left[\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\right]\ge0\)
Nhân vế theo vế ta được đpcm
Dấu \("="\Leftrightarrow a=b=c\)

a3+b3+c3= (a+b)3-3ab(a+b)+c3
Thay a+b=-c vào, ta được:
a3 + b3 +c3 = (-c)3 -3ab(-c) +c3 = 3abc (đpcm)

\(5,M=a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)\\ M=\left(a+b\right)\left[\left(a+b\right)^2-3ab\right]\\ M=1\left(1-3ab\right)=1-3ab\ge1-\dfrac{3\left(a+b\right)^2}{4}=1-\dfrac{3}{4}=\dfrac{1}{4}\\ M_{min}=\dfrac{1}{4}\Leftrightarrow a=b=\dfrac{1}{2}\)

Câu 5:
\(a+b=1\Rightarrow a=1-b\)
\(M=a^3+b^3=\left(1-b\right)^3+b^3=1-3b+3b^2-b^3+b^3\)
\(=1-3b+3b^2=3\left(b^2-b+\dfrac{1}{4}\right)+\dfrac{1}{4}=3\left(b-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\ge\dfrac{1}{4}\)
\(minM=\dfrac{1}{4}\Leftrightarrow a=b=\dfrac{1}{2}\)
Câu 7:
\(a^3+b^3+abc\ge ab\left(a+b+c\right)\)
\(\Leftrightarrow a^3+b^3+abc-ab\left(a+b+c\right)\ge0\)
\(\Leftrightarrow a^3+b^3-a^2b-ab^2\ge0\)
\(\Leftrightarrow a^2\left(a-b\right)-b^2\left(a-b\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)\left(a^2-b^2\right)\ge0\Leftrightarrow\left(a-b\right)^2\left(a+b\right)\ge0\)(đúng do a,b dương)
Dấu "=" xảy ra \(\Leftrightarrow a=b\)

5.
Với mọi a;b ta có: \(\left(a-b\right)^2\ge0\Rightarrow a^2+b^2\ge2ab\Rightarrow2a^2+2b^2\ge a^2+b^2+2ab\)
\(\Rightarrow2\left(a^2+b^2\right)\ge\left(a+b\right)^2\Rightarrow a^2+b^2\ge\dfrac{1}{2}\left(a+b\right)^2=\dfrac{1}{2}\)
\(M=a^3+b^3=\left(a+b\right)\left(a^2+b^2-ab\right)=a^2+b^2-ab\)
\(M=\dfrac{3}{2}\left(a^2+b^2\right)-\dfrac{1}{2}\left(a+b\right)^2=\dfrac{3}{2}\left(a^2+b^2\right)-\dfrac{1}{2}\ge\dfrac{3}{2}.\dfrac{1}{2}-\dfrac{1}{2}=\dfrac{1}{4}\)
\(M_{min}=\dfrac{1}{4}\) khi \(a=b=\dfrac{1}{2}\)
6.
Do \(a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)=2>0\)
Mà \(a^2-ab+b^2>0\Rightarrow a+b>0\)
Mặt khác với mọi a;b ta có:
\(\left(a-b\right)^2\ge0\Rightarrow a^2+b^2\ge2ab\Rightarrow a^2+b^2+2ab\ge4ab\)
\(\Rightarrow\left(a+b\right)^2\ge4ab\Rightarrow ab\le\dfrac{1}{4}\left(a+b\right)^2\) \(\Rightarrow-ab\ge-\dfrac{1}{4}\left(a+b\right)^2\)
Từ đó:
\(2=a^3+b^3=\left(a+b\right)^3-3ab\left(a+b\right)\ge\left(a+b\right)^3-3.\dfrac{1}{4}\left(a+b\right)^2\left(a+b\right)=\dfrac{1}{4}\left(a+b\right)^3\)
\(\Rightarrow\left(a+b\right)^3\le8\Rightarrow a+b\le2\)
\(N_{max}=2\) khi \(a=b=1\)

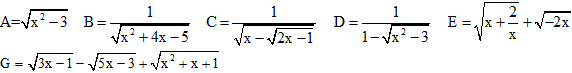 Mn giúp em với ;-;
Mn giúp em với ;-;
Áp dụng bất đẳng thức Bu- nhi -a ta có:
(a + b)2 \(\le\) 2. (a2 + b2)
=> (a + b)4 \(\le\) 4. (a2 + b2)2 = 4.\(\left(\sqrt{a}.a\sqrt{a}+\sqrt{b}.b\sqrt{b}\right)^2\le4.\left(\left(\sqrt{a}\right)^2+\left(\sqrt{b}\right)^2\right).\left(\left(a\sqrt{a}\right)^2+\left(b\sqrt{b}\right)^2\right)\)
= 4. (a + b) . (a3 + b3)
=> (a + b)4 \(\le\) 8.(a + b)
Vì a3 + b3 = (a + b). (a2 - ab + b2) = 2 Mà a2 - ab + b2 > 0 nên a + b > 0
Do đó, (a + b)3 \(\le\) 8 => a+ b \(\le\) 2
Dấu "=" khi a = b = 1