Cho đường thẳng
y=2x-6
cắt Ox tại A, Oy tại B. Độ dài đoạn AB gần nhất với số nào sau đây?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Xét phương trình hoành độ giao điểm của (C) và (d):
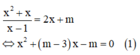

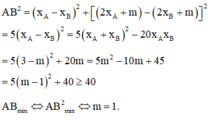


Xét tam giác ABO có: góc AOB+ góc ABO+ góc OAB= 180 độ( tổng 3 góc trong tam giác)
=> 60 độ+ góc ABO + 90 độ= 180 độ
=>góc ABO=30 độ
Gọi EK là đường trung trực của AB
Xét tam giác BEK có: góc BEK+ góc BKE+ góc KBE= 180 độ (tổng 3 góc trong tam giác)
=> góc BEK=60 độ

ta kẻ tia OP
vì OB//AP \(\Rightarrow\)góc AOB=OPB (slt)
góc BOP=ABO (slt)
xét 2 tam giác OAB và OBP
OP chung
AOP=OBP (cmt)
BOP=ABO (cmt)
vậy t.g OAB=OBP (g.c.g)
suy ra OA-=BP, OB=AP (2 cạnh tương ứng)
ta có OA//PB suy ra OAB=APB
xét 2 t.g OAI và IPB
OA=PB (cmt_
OAI=IBP
AOI=IPB
vậy 2 t.g OAI=IPB
vậy AI=IB
IO=IP
suy ra 2 đoạn thẳng cắt nhau tai trung điểm I của mỗi đoạn
\(y_A=0\Rightarrow2x_A-6=0\Rightarrow x_A=3\)
\(x_B=0\Rightarrow y_B=2.0-6=-6\)
Áp dụng định lý Pitago:
\(AB=\sqrt{x_A^2+y_B^2}=\sqrt{3^2+\left(-6\right)^2}=3\sqrt{5}\approx6,71\)