Một máy bay thực hiện chuyến bay theo hướng Nam – Bắc một quãng đường 1000 km mất 2h, rồi đổi hướng bay theo hướng Tây Nam được quãng đường 2000 km mất 2,5h. Tính độ lớn của độ dời của máy bay và góc hợp bởi độ dời với hướng Đông - Tây
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
11 tháng 6 2019
Đáp án là A
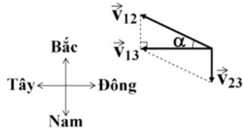
v 12 → là vận tốc của máy bay so với gió.
v 23 → là vận tốc của gió so với mặt đất.
v 13 → là vận tốc máy bay so với mặt đất.
- Ta có : v 13 → = v 12 → + v 23 → → v 13 → ⊥ v 23 → sinα = v 23 v 12 = 80 120
→ α = 23 , 6 0 .
QT
Quoc Tran Anh Le
Giáo viên
9 tháng 12 2023
(1) máy bay
(2) gió
(3) mặt đất
Ta có vận tốc của máy bay so với gió là v12 = 525 km/h; vận tốc của gió so với mặt đất là v23 = 36 km/h
Chọn chiều dương là chiều chuyển động của máy bay (hướng bắc)
Do gió chuyển động theo hướng nam nên: \(\overrightarrow {{v_{23}}} < 0\)
Vận tốc của máy bay là:
\(\begin{array}{l}\overrightarrow {{v_{13}}} = \overrightarrow {{v_{12}}} + \overrightarrow {{v_{23}}} \\ \Rightarrow {v_{13}} = {v_{12}} - {v_{23}} = 525 - 36 = 489(km/h)\end{array}\)
=> Thời gian bay của máy bay trên quãng đường 1160 km là:
\(t = \frac{S}{v} = \frac{{1160}}{{489}} \approx 2,37(h)\)
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
Vẽ vecto \(\overrightarrow {AB} \) là vecto vận tốc của máy bay, \(\overrightarrow {AD} \) là vecto vận tốc của gió.
Khi đó vecto vận tốc mới của máy bay là \(\overrightarrow {AB} + \overrightarrow {AD} \)
Dựng hình bình hành ABCD. Ta có: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Áp dụng định lí cosin trong tam giác ABC, ta có:
\(A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\)
Mà AB = 700, BC = AD = 40, \(\widehat B = {135^o}\)
\(\begin{array}{l} \Rightarrow A{C^2} = {700^2} + {40^2} - 2.700.40.\cos {135^o} \approx 531197,98\\ \Leftrightarrow AC \approx 728,83\end{array}\)
Vậy tốc độ mới của máy bay là 728,83 km/h.
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
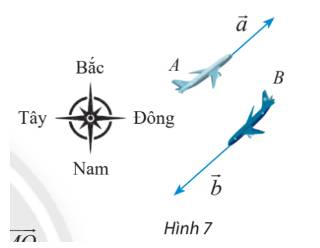
Vecto \(\overrightarrow a ,\;\overrightarrow b \) là vecto vận tốc của máy bay A và máy bay b.
Do đó \(\left| {\overrightarrow a } \right|,\;\left| {\overrightarrow b } \right|\) lần lượt là độ lớn của vecto vận tốc tương ứng.
Ta có: \(\left| {\overrightarrow a } \right| = 600,\;\left| {\overrightarrow b } \right| = 800\)
\( \Rightarrow \frac{{\left| {\overrightarrow b } \right|}}{{\left| {\overrightarrow a } \right|}} = \frac{{800}}{{600}} = \frac{4}{3}\)
Hai hướng Đông Bắc và Tây Nam là ngược nhau, do đó \(\overrightarrow b = - \frac{4}{3}\overrightarrow a \)
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
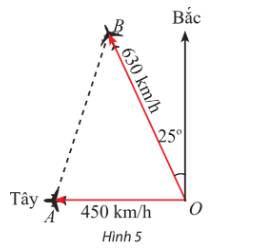
Ta có: \(\widehat {BOA} = {90^o} - {25^o} = {65^o}.\)
Sau 90 phút = 1,5 giờ:
Máy bay thứ nhất đi được quãng đường (OA) là: \(450.1,5 = 675\;(km)\)
Máy bay thứ hai đi được quãng đường (OB) là: \(630.1,5 = 945\;(km)\)
Áp dụng định lí cosin trong tam giác OAB, ta có:
\(\begin{array}{l}A{B^2} = O{A^2} + O{B^2} - 2OA.OB\cos O\\ \Leftrightarrow A{B^2} = {675^2} + {945^2} - 2.675.945\cos {65^o}\\ \Rightarrow AB \approx 900\end{array}\)
Vậy sau 90 phút, hai máy bay cách nhau khoảng 900 km.
VT
11 tháng 5 2019
Chọn C.
Kí hiệu: máy bay là vật 1, gió là vật 2 và mặt đất là vật 3 thì:
v12 = 120km/h và v23 = 50 km/h
Theo công thức cộng vận tốc:
