K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 7 2021
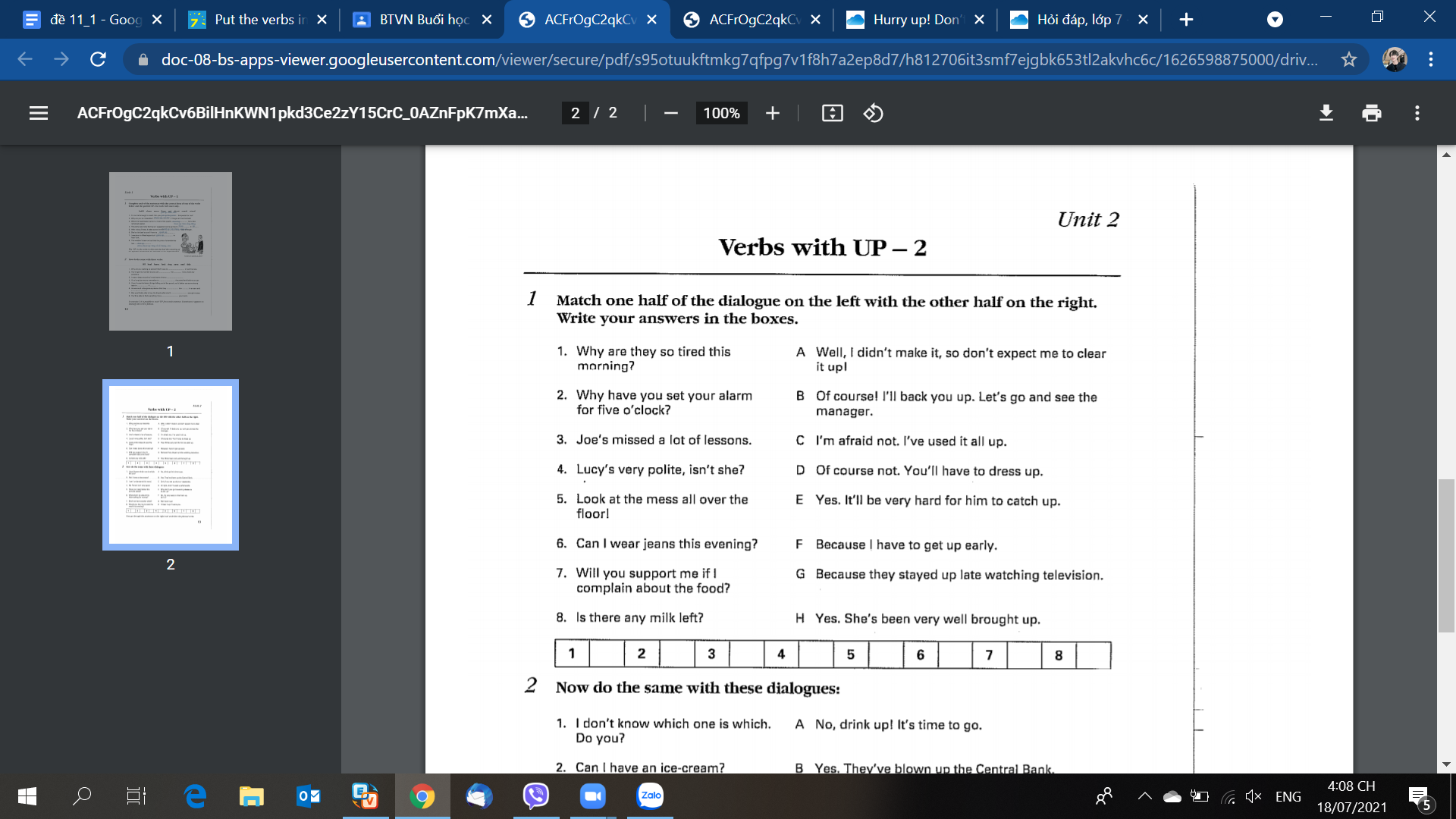
1.
1G 2F 3E 4H 5A 6D 7B 8C
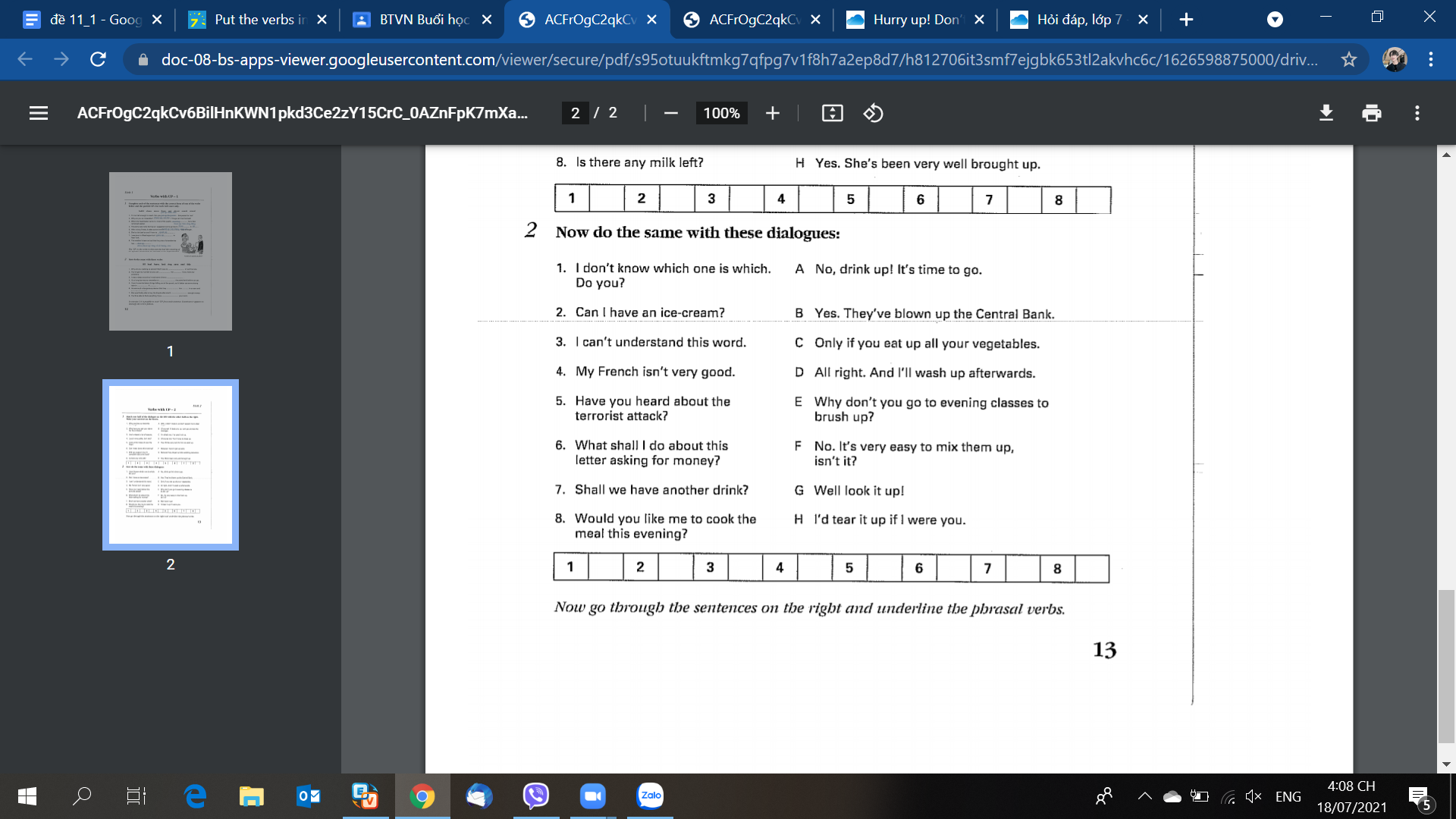
2.
1F 2C 3G 4E 5B 6H 7A 8D
2.
1 hurry up
2 ring me up
3 heal
4 fill up
5 seal it up
6 locked him up
7 saved up
8 tidy up
PA
0
1 tháng 7 2021
Bài 2:
a) Ta có: \(\dfrac{5\sqrt{2}-2\sqrt{5}}{\sqrt{5}-\sqrt{2}}+\dfrac{6}{2-\sqrt{10}}-\dfrac{20}{\sqrt{10}}\)
\(=\dfrac{\sqrt{10}\left(\sqrt{5}-\sqrt{2}\right)}{\sqrt{5}-\sqrt{2}}+\dfrac{6\cdot\left(\sqrt{10}+2\right)}{\left(\sqrt{10}-2\right)\left(\sqrt{10}+2\right)}-\dfrac{\sqrt{10}\cdot2\sqrt{10}}{\sqrt{10}}\)
\(=\sqrt{10}+\sqrt{10}-2-2\sqrt{10}\)
=-2
b) Ta có: \(\left(\dfrac{5-\sqrt{5}}{\sqrt{5}}-2\right)\left(\dfrac{4}{1+\sqrt{5}}+4\right)\)
\(=\left(\sqrt{5}-1-2\right)\left(\sqrt{5}-1+4\right)\)
\(=\left(\sqrt{5}-3\right)\left(\sqrt{5}+3\right)\)
=5-9=-4
c) Ta có: \(\dfrac{\sqrt{5}-\sqrt{3}}{\sqrt{5}+\sqrt{3}}+\dfrac{\sqrt{5}+\sqrt{3}}{\sqrt{5}-\sqrt{3}}-\dfrac{\sqrt{5}+1}{\sqrt{5}-1}\)
\(=\dfrac{\left(\sqrt{5}-\sqrt{3}\right)^2+\left(\sqrt{5}+\sqrt{3}\right)^2}{\left(\sqrt{5}+\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)}-\dfrac{\left(\sqrt{5}+1\right)^2}{\left(\sqrt{5}-1\right)\left(\sqrt{5}+1\right)}\)
\(=\dfrac{8-2\sqrt{15}+8+2\sqrt{15}}{2}-\dfrac{6+2\sqrt{5}}{4}\)
\(=\dfrac{16}{2}-\dfrac{6+2\sqrt{5}}{4}\)
\(=\dfrac{32-6-2\sqrt{5}}{4}\)
\(=\dfrac{26-2\sqrt{5}}{4}\)
\(=\dfrac{13-\sqrt{5}}{2}\)
20 tháng 8 2021
Bài 3:
c: Ta có: \(3x-5-5\sqrt{x-1}=0\)
\(\Leftrightarrow5\sqrt{x-1}=3x-5\)
\(\Leftrightarrow25x-25=9x^2-30x+25\)
\(\Leftrightarrow9x^2-55x+50=0\)
\(\text{Δ}=\left(-55\right)^2-4\cdot9\cdot50=1225\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{55-35}{18}=\dfrac{10}{9}\\x_2=\dfrac{55+35}{18}=5\end{matrix}\right.\)
17 tháng 5 2022
a: Xét ΔBDC có \(\widehat{BDC}>90^0\)
nên BC là cạnh lớn nhất
=>BC>BD
b: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó;ΔABD=ΔEBD
c: Xét ΔABC có
AK là phân giác
BD là phân giác
AK cắt BD tại O
Do đó: O là tâm đường tròn nội tiếp ΔABC
=>CO là phân giác của góc ACB
Xét ΔOHC vuông tại H và ΔOKC vuông tại K có
CO chung
\(\widehat{HCO}=\widehat{KCO}\)
Do đó: ΔOHC=ΔOKC
Suy ra: OH=OK
5 tháng 1 2022
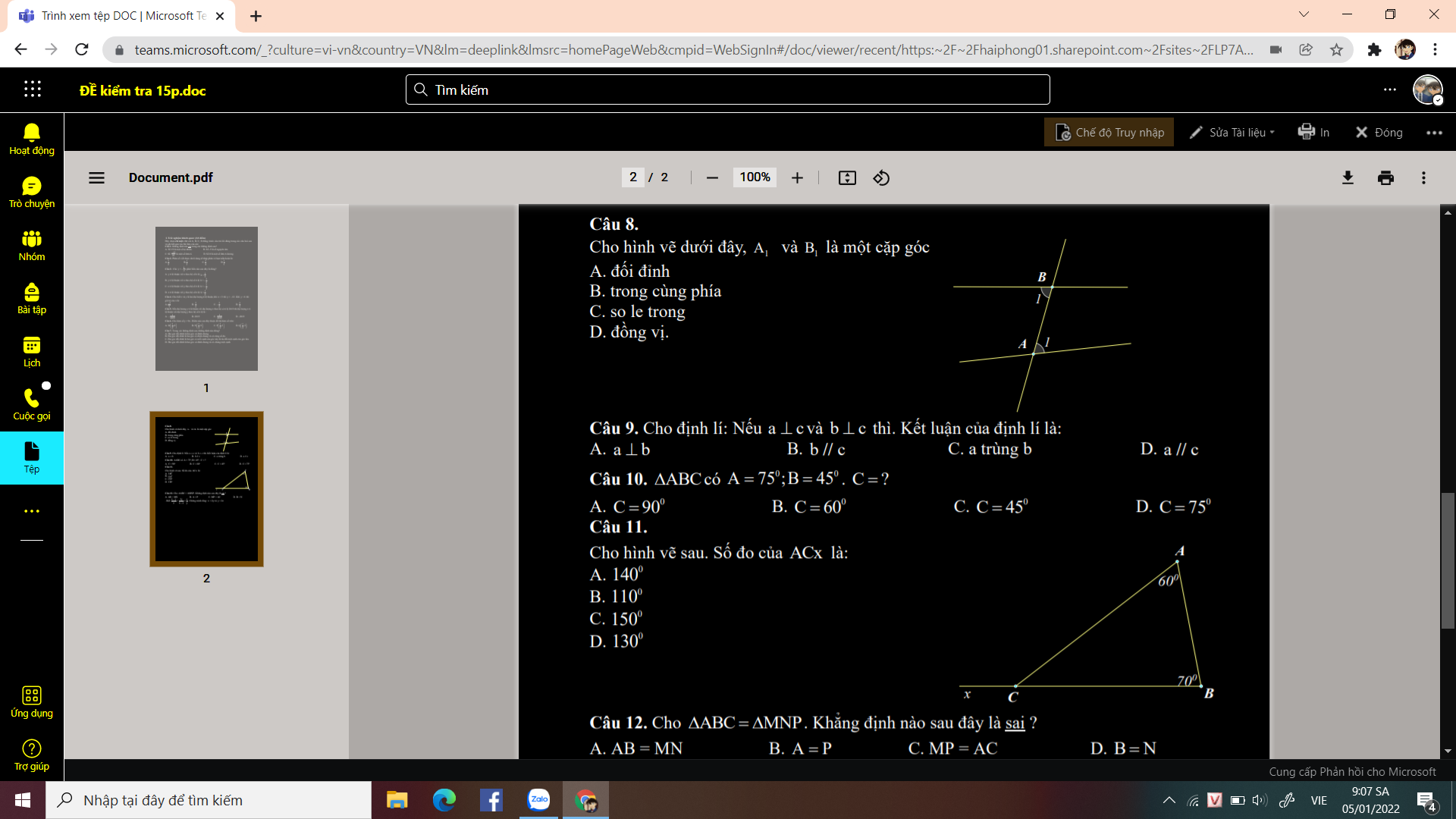
\(\text{8.C.So le trong}\)
\(\text{9.C.a trùng b}\)
\(\text{10.B.}60^0\)
\(\text{11.C.}150^0\)
\(\text{12.B.A=P}\)
PK
3
NT
3
NT
0
\(x\ge\frac{3}{2}\)
\(\sqrt{4x^2-9}=2\sqrt{2x+3}\)
\(\sqrt{2x-3}\sqrt{2x+3}=2\sqrt{2x+3}\)
dễ thấy \(\sqrt{2x+3}>0\)
\(\sqrt{2x-3}=2\)
\(2x-3=4\)
\(x=\frac{7}{2}\left(TM\right)\)
\(b,ĐKXĐ:x\ge\frac{3}{5}\)
\(\sqrt{25x^2-9}=2\sqrt{5x-3}\)
\(\sqrt{5x+3}\sqrt{5x-3}=2\sqrt{5x-3}\)
\(\sqrt{5x-3}\ge0\)
\(TH1:\sqrt{5x-3}=0\)
\(x=\frac{3}{5}\)
\(\sqrt{5.\frac{3}{5}+3}.0=2.0\)pt (luôn đúng<=> vô số nghiệm)
\(TH2:\sqrt{5x-3}>0\)
\(\sqrt{5x+3}\sqrt{5x-3}=2\sqrt{5x-3}\)
\(\sqrt{5x+3}=2\)
\(x=\frac{1}{5}\left(KTM\right)\)vì \(ĐKXĐ:x\ge\frac{3}{5}\)