Tìm số tự nhiên a,biết a<200 khi lấy a chia 2 dư 1, a chia 3 dư 1, chia cho 5 dư 4 và chia hết cho 7.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
3 tháng 10 2023
1) 12 = 1.12 = 2.6 = 3.4 = 4.3 = 6.2 = 12.1
2) 12 = 1.12 = 2.6 = 3.4
Vậy (a; b) ∈ {(1; 12); (2; 6); (3; 4)}
3) 30 = 1.30 = 2.15 = 3.10 = 5.6 = 6.5 = 10.3 = 15.2 = 30.1
4) 30 = 30.1 = 15.2 = 10.3 = 6.5
Vậy (a; b) ∈ {(30; ); (15; 2); (10; 3); (6; 5)}
3 tháng 10 2023
a, Ta có: 12 = 1 x 12; 2 x 6; 3 x 4
b, Ta có: 12 = 1 x 12; 2 x 6; 3x 4
Theo đề bài, ta có điều kiện: a < b
=> a ϵ {1; 2; 3}
=> b ϵ {12; 6; 4}
Vậy các cặp số (a; b) cần tìm là:
(a; b) ϵ {(1; 12); (2; 6); (3; 4)}
c, Ta có: 30 = 1 x 30; 2 x 15; 3 x 10; 5 x 6
d, Ta có: 30 = 1 x 30; 2 x 15; 3 x 10; 5 x 6
Theo đề bài, ta có điều kiện: a > b
=> a = 30; b = 1
=> a = 15; b = 2
=> a = 10; b = 3
=> a = 6; b = 5
Vậy ta có các cặp số (a; b) thỏa mãn đề bài là:
(a; b) ϵ {(30; 1); (15; 2); (10; 3); (6; 5}
3 tháng 12 2023
a:
\(70=2\cdot5\cdot7;84=2^2\cdot3\cdot7\)
=>\(ƯCLN\left(70;84\right)=2\cdot7=14\)
=>\(ƯC\left(70;84\right)=Ư\left(14\right)=\left\{1;2;7;14\right\}\)
\(70⋮x;84⋮x\)
=>\(x\inƯC\left(70;84\right)\)
=>\(x\inƯ\left(14\right)\)
=>\(x\in\left\{1;2;7;14\right\}\)
mà x>8
nên x=14
b: \(35=5\cdot7;45=3^2\cdot5\)
=>\(BCNN\left(35;45\right)=3^2\cdot5\cdot7=9\cdot35=315\)
\(a⋮35;a⋮45\)
=>\(a\in BC\left(35;45\right)\)
=>\(a\in B\left(315\right)\)
=>\(a\in\left\{315;630;945;...\right\}\)
mà 500<a<900
nên a=630
3 tháng 12 2023
A) Để tìm số tự nhiên x, ta cần tìm ước chung lớn nhất của 70 và 84. Ta có:
70 : x = 84 : x
Đặt ước chung lớn nhất của 70 và 84 là d. Ta có:
70 = d * m1
84 = d * m2
Trong đó m1 và m2 là các số tự nhiên. Ta thấy d là ước chung lớn nhất của 70 và 84 khi và chỉ khi d là ước chung lớn nhất của m1 và m2.
Ta phân tích 70 và 84 thành các thừa số nguyên tố:
70 = 2 * 5 * 7
84 = 2^2 * 3 * 7
Ta thấy ước chung lớn nhất của 70 và 84 là 2 * 7 = 14.
Vì x > 8, nên x = 14.
B) Để tìm số tự nhiên a, ta cần tìm ước chung lớn nhất của a và 35, cũng như ước chung lớn nhất của a và 45. Ta có:
a : 35 = a : 45
Đặt ước chung lớn nhất của a và 35 là d1, và ước chung lớn nhất của a và 45 là d2. Ta có:
a = d1 * m1
a = d2 * m2
Trong đó m1 và m2 là các số tự nhiên. Ta thấy a là số tự nhiên khi và chỉ khi a là ước chung lớn nhất của m1 và m2.
Ta phân tích 35 và 45 thành các thừa số nguyên tố:
35 = 5 * 7
45 = 3^2 * 5
Ta thấy ước chung lớn nhất của 35 và 45 là 5.
Vì 500 < a < 900, nên a = 5.
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
20 tháng 7 2023
a bằng giá trị trung bình cộng của 7,11 và a. Vì vậy a có giá trị bằng trung bình cộng của 7 và 11.
Số tự nhiên a cần tìm là:
(7+11):2=9
Đáp số: a là 9
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
10 tháng 4 2023
Giải toán bằng sơ đồ đoạn thẳng của tiểu học em nhé
Tổng của hai số 7 và 11 là: 7 + 11 = 18
Coi trung bình cộng của ba số là 1 phần ta có sơ đồ
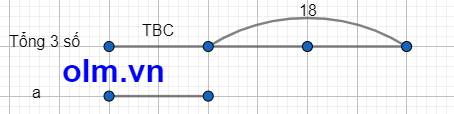
theo sơ đồ ta có:
Số tự nhiên a là: 18 : 2 = 9
Đáp số: 9
18 tháng 11 2021
- Ta có: a ≥ b ( a,b ∈ N )
ƯCLN ( a, b) = 16
⟹ a chia hết cho 16 ⟹ a = 16.m
⟹ b chia hết cho 16 ⟹ b = 16. n
(m, n là thương; m,n ∈ N, m ≥ n)
ƯCLN(m,n) = 1
⟹ a . b = ƯCLN.BCNN
mà a = 16. m
b = 16. n
Thay số: 16 . m . 16 . n = 16 . 240
16. m . 16. n = 3840
256. m. n = 3840
⟹ m. n = 3840 : 256 = 15
Ta có bảng sau :
| m | ... | ... | ... |
| n | ... | ... | ... |
| a | ... | ... | ... |
| b | ... | ... | ... |
⟹ Vậy (a,b) ∈ { (... , ...) ; (... , ....)}
R
24 tháng 11 2021
\(a=0;1;2;3\) ở câu a
\(a=0;1;2;3;4;5;6;7\) ở câu b
\(a=0;1;2;3;4;5;6\) ở câu c
24 tháng 7 2023
a) Vì 13, 15,61 chia cho a đều dư 1 => 13;15;61 \(⋮a-1\)
=> a-1 thuộc ƯC(13;15;61)
Mà a lớn nhất => a-1 thuộc ƯCLN(13,15,61)
Mà 13;15;61 là các số nguyên tố cùng nhau => ƯCLN(13;15;61) = 1
=> a-1=1
=>a=2
Vậy a=2.
b) Ta có: 149 : a dư 29 => (149-29) thì chia hết cho a ( a > 29)
235 : a dư 35 => ( 235 - 35) chia hết cho a ( a> 35)
=> a thuộc ƯCLN(120,200) = 40
=> a = 40
Vậy a = 40
c) câu c tương tự câu b