Chỉ e với mn ơi
Gấp ạ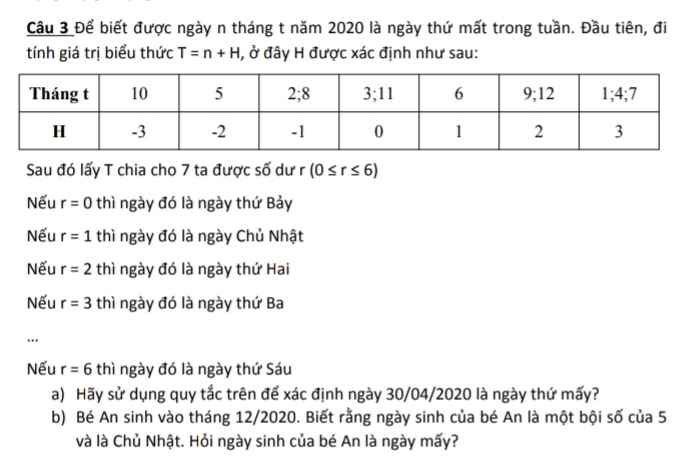
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 2 2023
1.Yes, they do
2..Yes, it is
3.People buy fruits and flowers from the market and decorate their house
4.People visit their family and friends
giúp em với mn ơi,e đag cần gấp, mn giúp em với ạ
31 tháng 10 2021
a: Xét ΔBAC có
D là trung điểm của AB
M là trung điểm của AC
Do đó: DM là đường trung bình của ΔABC
Suy ra: DM//BC và \(DM=\dfrac{BC}{2}=3.5\left(cm\right)\)
QA
0
LT
3
KY
4 tháng 2 2023
1, That
2, This
3, that
4, those
5, these - that
6, these
7, this
8, that
9, that
10, this
11, those
12, this
13, it
14, these
15, them
16, those
B
18 tháng 1 2023
1 friendly
2 creative
3 boring
4 funny
5 sensitive
6 outgoing
7 lazy
8 impatient
9 active
10 quiet
NT
2
24 tháng 11 2023
Câu 8.
a)\(R_1//R_2\Rightarrow R_{12}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{18\cdot12}{18+12}=7,2\Omega\)
\(I=\dfrac{U}{R}=\dfrac{18}{7,2}=2,5A\)
\(U_1=U_2=U=18V\)
\(I_1=\dfrac{U_1}{R_1}=\dfrac{18}{18}=1A\)
\(I_2=I-I_1=2,5-1=1,5A\)
\(P_m=\dfrac{U_m^2}{R_{tđ}}=\dfrac{18^2}{7,2}=45W\)
b)Chiều dài dây \(l_1\) là: \(R_1=\rho\cdot\dfrac{l_1}{S_1}\)
\(\Rightarrow18=1,7\cdot10^{-8}\cdot\dfrac{l_1}{0,01\cdot10^{-8}}\Rightarrow l_1=\dfrac{9}{85}m\approx0,106m\)
c)Công suất tiêu thụ của đoạn mạch tăng gấp đôi: \(P_m=2\cdot45=90W\)
Điện trở tương đương: \(R_{tđ}=\dfrac{U^2}{P_m}=\dfrac{18^2}{90}=3,6\)
Thay đề bài thành
\(R_3//R_{12}\Rightarrow R_{tđ}=\dfrac{R_3\cdot R_{12}}{R_3+R_{12}}=\dfrac{R_3\cdot7,2}{R_3+7,2}=3,6\Rightarrow R_3=7,2\Omega\)
Câu 9.
\(R_đ=\dfrac{U_1^2}{P_1}=\dfrac{220^2}{100}=484\Omega;I_đ=\dfrac{P_1}{U_1}=\dfrac{100}{220}=\dfrac{5}{11}A\)
\(R_b=\dfrac{U_2^2}{P_2}=\dfrac{220^2}{600}=\dfrac{242}{3}\Omega;I_b=\dfrac{P_2}{U_2}=\dfrac{600}{220}=\dfrac{30}{11}A\)
\(R_q=\dfrac{U_3^2}{P_3}=\dfrac{220^2}{110}=440\Omega;I_q=\dfrac{P_3}{U_3}=\dfrac{110}{220}=0,5A\)
a)\(R_{tđ}=R_1+R_2+R_3=484+\dfrac{242}{3}+440=\dfrac{3014}{3}\Omega\)
\(I_1=I_2=I_3=I=\dfrac{U}{R_{tđ}}=\dfrac{220}{\dfrac{3014}{3}}=\dfrac{30}{137}A\approx0,22A\)
b)Điện năng mà các vật tiêu thụ trong 30 ngày là:
\(A_đ=\dfrac{U_đ^2}{R_đ}\cdot t=\dfrac{220^2}{484}\cdot6\cdot3600\cdot30=64800000J=18kWh\)
\(A_b=\dfrac{U_b^2}{R_b}\cdot t=\dfrac{220^2}{\dfrac{242}{3}}\cdot3\cdot3600\cdot30=194400000J=54kWh\)
\(A_q=\dfrac{U^2_q}{R_q}\cdot t=\dfrac{220^2}{440}\cdot10\cdot3600\cdot30=118800000J=33kWh\)
\(A=A_đ+A_b+A_q=18+54+33=105kWh\)
TM
24 tháng 11 2023
Câu 8. \(R_1\left|\right|R_2\)
(a) Cường độ dòng điện qua các điện trở:
\(\left\{{}\begin{matrix}I_1=\dfrac{U}{R_1}=\dfrac{18}{18}=1\left(A\right)\\I_2=\dfrac{U}{R_2}=\dfrac{18}{12}=1,5\left(A\right)\end{matrix}\right.\)
Công suất của mạch: \(P=\dfrac{U^2}{R}=\dfrac{U^2}{\dfrac{R_1R_2}{R_1+R_2}}=\dfrac{18^2}{\dfrac{18\cdot12}{18+12}}=45\left(W\right)\)
(b) \(S=0,01\left(mm^2\right)=10^{-8}\left(m^2\right)\)
Chiều dài dây: \(R_1=\rho\cdot\dfrac{l}{S}\Rightarrow l=\dfrac{R_1S}{\rho}=\dfrac{18\cdot10^{-8}}{1,7\cdot10^{-8}}\approx10,59\left(m\right)\)
(c) Đề sai.
8 tháng 5 2021
ĐKXĐ: \(x\notin\left\{0;-9\right\}\)
Ta có: \(\dfrac{1}{x+9}-\dfrac{1}{x}=\dfrac{1}{5}+\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{20x}{20x\left(x+9\right)}-\dfrac{20\left(x+9\right)}{20x\left(x+9\right)}=\dfrac{4x\left(x+9\right)+5x\left(x+9\right)}{20x\left(x+9\right)}\)
Suy ra: \(4x^2+36x+5x^2+45x=20x-20x-180\)
\(\Leftrightarrow9x^2+81x+180=0\)
\(\Leftrightarrow x^2+9x+20=0\)
\(\Leftrightarrow x^2+4x+5x+20=0\)
\(\Leftrightarrow x\left(x+4\right)+5\left(x+4\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+4=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\left(nhận\right)\\x=-5\left(nhận\right)\end{matrix}\right.\)
Vậy: S={-4;-5}
KH
8 tháng 5 2021
Hướng làm:
Thấy cả tử mẫu cộng lại đều bằng 2021 → Cộng thêm 1 rồi quy đồng với mỗi phân thức
\(\dfrac{x+2}{2019}+1+\dfrac{x+3}{2018}+1=\dfrac{x+4}{2017}+1+\dfrac{x}{2021}+1\\ \Leftrightarrow\dfrac{x+2021}{2019}+\dfrac{x+2021}{2018}-\dfrac{x+2021}{2017}-\dfrac{x+2021}{2021}=0\\ \Leftrightarrow\left(x+2021\right)\left(\dfrac{1}{2019}+\dfrac{1}{2018}-\dfrac{1}{2017}-\dfrac{1}{2021}\right)=0\\ \Leftrightarrow x+2021=0\Leftrightarrow x=-2021\)
TM
8 tháng 5 2021
\(< =>\dfrac{x+2}{2019}+1+\dfrac{x+3}{2018}+1=\dfrac{x+4}{2017}+1+\dfrac{x}{2021}+1\)
\(< =>\dfrac{x+2+2019}{2019}+\dfrac{x+3+2018}{2018}=\dfrac{x+4+2017}{2017}+\dfrac{x+2021}{2021}\)
\(< =>\dfrac{x+2021}{2019}+\dfrac{x+2021}{2018}-\dfrac{x+2021}{2017}-\dfrac{x+2021}{2021}=0\)
\(< =>\left(x+2021\right)\left(\dfrac{1}{2019}+\dfrac{1}{2018}-\dfrac{1}{2017}-\dfrac{1}{2021}=\right)=0\)
\(< =>x+2021=0< =>x=-2021\)
Vậy....