Cho 2 số dương a,b có a + b = 1
2/ab + 3/(a^2 + b^2) >= 14
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NH
Nguyễn Huy Tú
14 tháng 7 2021
Đúng(0)
Những câu hỏi liên quan
CT
2
TN
10 tháng 8 2017
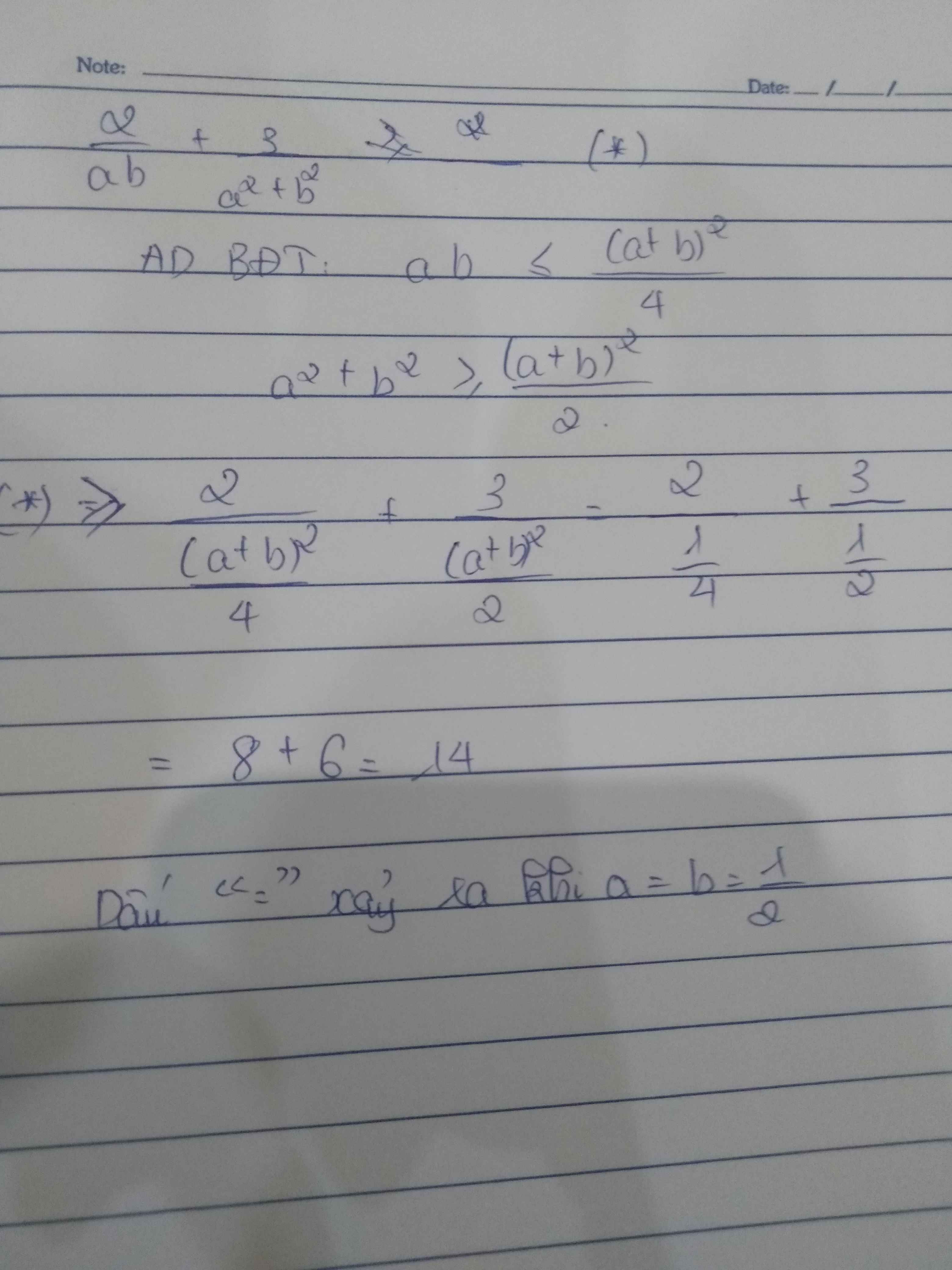
ko sai nhé
Áp dụng BĐT Cauchy-Schwarz dạng ENgel ta có:
\(VT=\frac{3}{ab+bc+ca}+\frac{2}{a^2+b^2+c^2}\)
\(=\frac{\sqrt{6}^2}{2\left(ab+bc+ca\right)}+\frac{\sqrt{2}^2}{a^2+b^2+c^2}\)
\(\ge\frac{\left(\sqrt{6}+\sqrt{2}\right)^2}{a^2+b^2+c^2+2\left(ab+bc+ca\right)}\)
\(=\frac{\left(\sqrt{6}+\sqrt{2}\right)^2}{\left(a+b+c\right)^2}\approx15>14\)
16 tháng 5 2018
Câu a dùng hằng đẳng thức mở rộng là được,tối rồi lười lắm,t giúp câu b
V
0
1 tháng 9 2020
Câu a bạn chứng minh được rồi là xong nha !!!!!!!
Câu b)
\(B=\frac{\left(a+b+c\right)^2}{ab+bc+ca}+\frac{ab+bc+ca}{\left(a+b+c\right)^2}\)
\(B=\frac{\left(a+b+c\right)^2}{9\left(ab+bc+ca\right)}+\frac{ab+bc+ca}{\left(a+b+c\right)^2}+\frac{8\left(a+b+c\right)^2}{9\left(ab+bc+ca\right)}\)
Ta lần lượt áp dụng BĐT Cauchy 2 số và sử dụng câu a sẽ được:
=> \(B\ge2\sqrt{\frac{\left(a+b+c\right)^2\left(ab+bc+ca\right)}{9\left(ab+bc+ca\right)\left(a+b+c\right)^2}}+\frac{8.3\left(ab+bc+ca\right)}{9\left(ab+bc+ca\right)}\)
=> \(B\ge\frac{2}{3}+\frac{8}{3}=\frac{10}{3}\)
DẤU "=" Xảy ra <=> \(a=b=c\)
Vậy ta có ĐPCM !!!!!!!!
NV
0
QT
19 tháng 5 2018
\(\sum\dfrac{a}{b^2+bc+c^2}\ge\dfrac{\left(a+b+c\right)^2}{ab^2+abc+ac^2+bc^2+abc+ba^2+ca^2+abc+cb^2}=\dfrac{\left(a+b+c\right)^2}{\left(a+b+c\right)\left(ab+bc+ac\right)}=\dfrac{a+b+c}{ab+bc+ac}\)
FF
28 tháng 8 2016
3. abc > 0 nên trog 3 số phải có ít nhất 1 số dương.
Vì nếu giả sử cả 3 số đều âm => abc < 0 => trái giả thiết
Vậy nên phải có ít nhất 1 số dương
Không mất tính tổng quát, giả sử a > 0
mà abc > 0 => bc > 0
Nếu b < 0, c < 0:
=> b + c < 0
Từ gt: a + b + c < 0
=> b + c > - a
=> (b + c)^2 < -a(b + c) (vì b + c < 0)
<=> b^2 + 2bc + c^2 < -ab - ac
<=> ab + bc + ca < -b^2 - bc - c^2
<=> ab + bc + ca < - (b^2 + bc + c^2)
ta có:
b^2 + c^2 >= 0
mà bc > 0 => b^2 + bc + c^2 > 0
=> - (b^2 + bc + c^2) < 0
=> ab + bc + ca < 0 (vô lý)
trái gt: ab + bc + ca > 0
Vậy b > 0 và c >0
=> cả 3 số a, b, c > 0
3 tháng 5 2019
1.a, Ta có: \(\left(a+b\right)^2\ge4a>0\)
\(\left(b+c\right)^2\ge4b>0\)
\(\left(a+c\right)^2\ge4c>0\)
\(\Rightarrow\left[\left(a+b\right)\left(b+c\right)\left(a+c\right)\right]^2\ge64abc\)
Mà abc=1
\(\Rightarrow\left[\left(a+b\right)\left(b+c\right)\left(a+c\right)\right]^2\ge64\)
\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(a+c\right)\ge8\left(đpcm\right)\)
AH
Akai Haruma
Giáo viên
14 tháng 5 2019
Lời giải:
Đặt:
\(A=\frac{3}{ab+bc+ac}+\frac{2}{a^2+b^2+c^2}=\frac{3}{ab+bc+ac}+\frac{2}{(a+b+c)^2-2(ab+bc+ac)}=\frac{3}{ab+bc+ac}+\frac{2}{1-2(ab+bc+ac)}\)
Đặt \(ab+bc+ac=t\Rightarrow A=\frac{3}{t}+\frac{2}{1-2t}\)
Theo hệ quả quen thuộc của BĐT AM-GM:
\(1=(a+b+c)^2\geq 3(ab+bc+ac)\Rightarrow t=ab+bc+ac\leq \frac{1}{3}\)
Xét:
\(A-14=\frac{3}{t}+\frac{2}{1-2t}=\frac{3}{t}-9+\frac{2}{1-2t}-5\)
\(=\frac{3-9t}{t}+\frac{10t-3}{1-2t}>\frac{3-9t}{t}+\frac{9t-3}{1-2t}=3(1-3t)(\frac{1}{t}-\frac{1}{1-2t})=\frac{3(1-3t)^2}{t(1-2t)}>0\) với mọi \(t>0; t\leq \frac{1}{3}\)
Do đó: \(A>14\) (đpcm).