Giúp mình giải bài 3 chi tiết nha
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 5 2021
Ta có
\(a^2+1=a^2+ab+bc+ca=a\left(a+b\right)+c\left(a+b\right)=\left(a+b\right).\left(a+c\right)\\ Cmtt:b^2+1=\left(b+a\right).\left(b+c\right)\\ c^2+1=\left(c+a\right).\left(c+b\right)\)
Nên
\(\dfrac{b-c}{a^2+1}+\dfrac{c-a}{b^2+1}+\dfrac{a-b}{c^2+1}\\ =\dfrac{\left(b-c\right)}{\left(a+b\right)\left(a+c\right)}+\dfrac{\left(c-a\right)}{\left(b+c\right)\left(b+a\right)}+\dfrac{\left(a-b\right)}{\left(c+a\right)\left(c+b\right)}\\ =\dfrac{\left(b-c\right)\left(b+c\right)+\left(c-a\right)\left(c+a\right)+\left(a-b\right)\left(a+b\right)}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\\ =\dfrac{b^2-c^2+c^2-a^2+a^2-b^2}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\\ =0\)
26 tháng 5 2021
\(\dfrac{b-c}{a^2+1}+\dfrac{c-a}{b^2+1}+\dfrac{a-b}{c^2+1}\)
\(=\dfrac{b-c}{a^2+ab+bc+ac}+\dfrac{c-a}{b^2+ab+bc+ca}+\dfrac{a-b}{c^2+ab+bc+ca}\)
\(=\dfrac{b-c}{a\left(a+b\right)+c\left(a+b\right)}+\dfrac{c-a}{b\left(a+b\right)+c\left(a+b\right)}+\dfrac{a-b}{c\left(c+a\right)+b\left(a+c\right)}\)
\(=\dfrac{b-c}{\left(a+c\right)\left(a+b\right)}+\dfrac{c-a}{\left(b+c\right)\left(a+b\right)}+\dfrac{a-b}{\left(b+c\right)\left(a+c\right)}\)
\(=\dfrac{\left(b-c\right)\left(b+c\right)+\left(c-a\right)\left(a+c\right)+\left(a-b\right)\left(a+b\right)}{\left(a+c\right)\left(a+b\right)\left(b+c\right)}\)
\(=\dfrac{b^2-c^2+c^2-a^2+a^2-b^2}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}=0\)
15 tháng 9 2021
1: \(100-x^2=\left(10-x\right)\left(10+x\right)\)
2: \(b^2-a^2=\left(b-a\right)\left(b+a\right)\)
3: \(\left(3y\right)^2-\left(4x\right)^2=\left(3y-4x\right)\left(3y+4x\right)\)
AT
1
12 tháng 1 2023
Bài 3:
a: \(=\left(-47+47\right)+\left(200-400\right)=-200\)
b: \(=\left(-2\right)+\left(-2\right)+\left(-2\right)=-6\)
c: \(=25\left(-19-81\right)=25\cdot\left(-100\right)=-2500\)
d: \(=17\cdot28-17\cdot32-28\cdot17+28\cdot32=32\cdot11=352\)
e: \(=12-57+57-12=0\)
HL
1
17 tháng 10 2021
b: Ta có: \(\dfrac{x+2}{5}=\dfrac{3-2x}{11}\)
\(\Leftrightarrow11x+22=15-10x\)
hay \(x=-\dfrac{1}{3}\)
N
1
18 tháng 7 2015
Số các số hạng của dãy số trên là:
81:(1+3+5)=9 số hạng
=> ta có dãy số như sau:
1+3+5+7+9+11+13+15+17
Vậy X là số hạng cuối cùng nên X=17
Giúp mình với aa (Giải chi tiết + nếu được thì thêm lời giải thích ở cuối bài làm giúp mình nha 
)
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
\(2\left(x-3\right)^4-3^2=503\\ \Rightarrow2\left(x-3\right)^4=512\\ \Rightarrow\left(x-3\right)^4=256\\ \Rightarrow\left[{}\begin{matrix}x-3=4\\x-3=-4\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=7\\x=-1\end{matrix}\right.\)
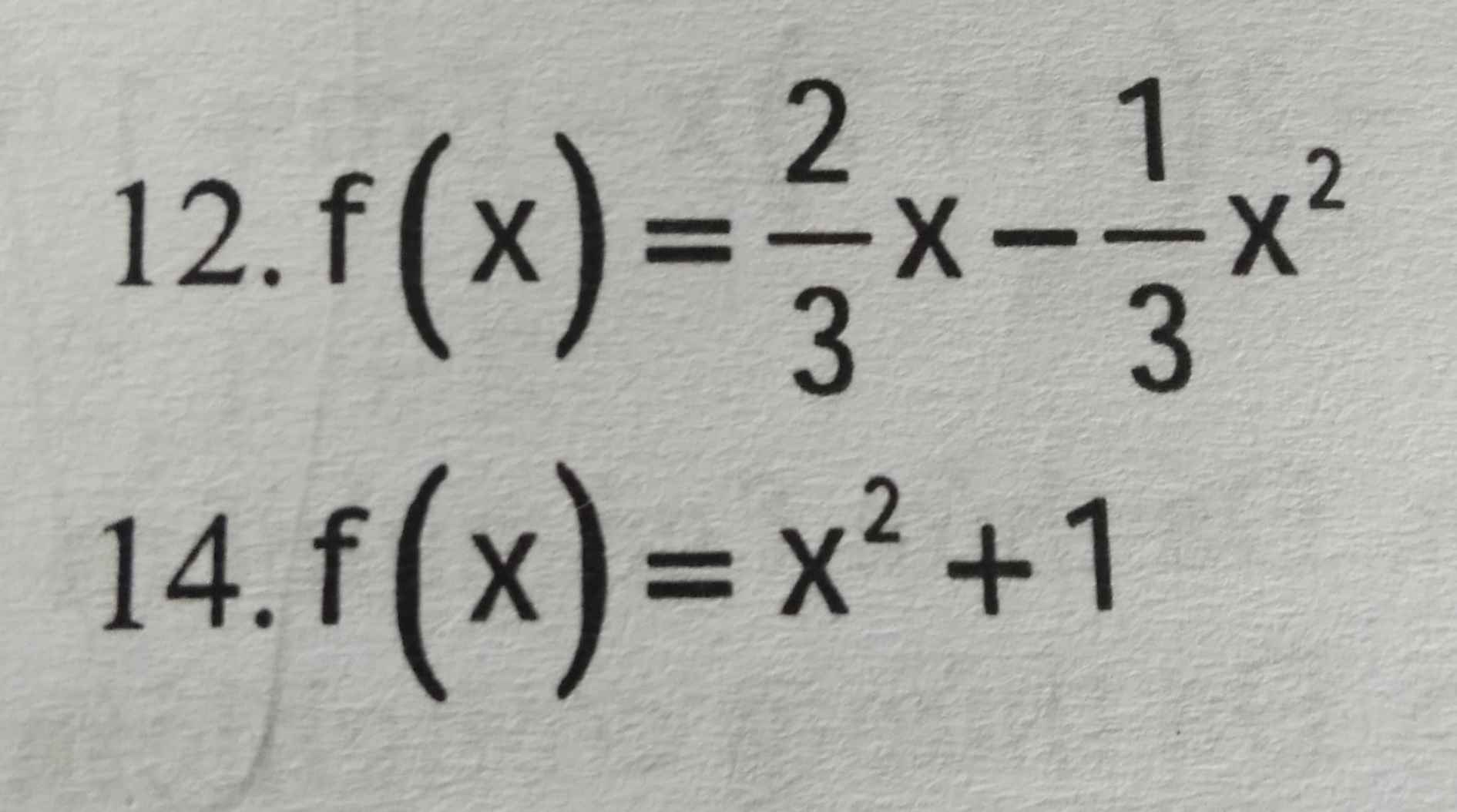
- Với \(m=1\) BPT trở thành \(2>0\) (thỏa mãn) (1)
- Với \(m\ne1\) tập nghiệm của BPT là R khi và chỉ khi:
\(\left\{{}\begin{matrix}m-1>0\\\Delta'=\left(m-1\right)^2-2\left(m-1\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>1\\\left(m-1\right)\left(m-3\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>1\\1< m< 3\end{matrix}\right.\)
\(\Leftrightarrow1< m< 3\) (2)
Kết hợp (1) và (2): với \(1\le m< 3\) thì BPT có tập nghiệm R