Rut gon, dự đoán: A= 12+22+32+.......n2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
E
21 tháng 1 2022
Với A1 = 12. Ta sẽ chứng minh An =1 + 3 + ... + (2n-1) = n2 (đáp án d)
Giả sử An đúng với n = k tức Ak = 1 + 3 + ... + (2k - 1) = k2. Ta sẽ chứng minh nó cũng đúng với Ak+1
Thật vậy: Ak+1 = 1 + 3 + ... + (2k-1) + (2k+1) = Ak + 2k + 1 = k2 + 2k + 1 = (k+1)2
Vậy...
DD
1
HN
29 tháng 11 2021
D=1212+2222+3232+....+ n2n2
D=1+ 2.(1+1) + 3.(2+1) +.....+ n(n-1 +1)
D=1 + 1.2 +2 + 2.3 + 3 +.......+ (n-1).n + n
D= (1 + 2 +3 +....+n) + (1.2 + 2.3 + 3.4 + ......+ (n-1)n )
D= n(n+1)2n(n+1)2 + n(n+1)(n−1)3n(n+1)(n−1)3
D= 3n(n+1)+2n(n+1)(n−1)63n(n+1)+2n(n+1)(n−1)6
D= n(n+1)(2n+1)6
26 tháng 5 2022
\(A=\dfrac{\dfrac{3}{8}-\dfrac{3}{10}+\dfrac{3}{11}+\dfrac{3}{12}}{\dfrac{-5}{8}+\dfrac{5}{10}-\dfrac{5}{11}-\dfrac{5}{12}}=\dfrac{-3}{5}\)
PT
1
28 tháng 1 2016
Phân số tối giản là: 5/7, 23/24
Phân số rút gọn là: 6/9, 12/24, 6/14
6/9=2/3 12/24=1/2 6/14=3/7
28 tháng 11 2021
TK
S=1.4+2.5+3.6+4.7+....+n.(n+3) S = 1. ( 2 + 2 ) + 2. ( 3 + 2 ) + 3. ( 4 + 2 ) + . . . + n . [ ( n + 1 ) + 2 ] S = 1.2 + 2.3 + 3.4 + . . . . + n . ( n + 1 ) + ( 1.2 + 2.2 + 3.2 + . . . . + n .2 ) Đặt A = 1.2 + 2.3 + 3.4 + . . . . + n . ( n + 1 ) 3 A = 1.2.3 + 2.3. ( 4 − 1 ) + . . . . + n . ( n + 1 ) . [ ( n + 2 ) − ( n − 1 ) 3 A = 1.2.3 + 2.3.4 − 1.2.3 + . . . . + n . ( n + 1 ) . ( n + 2 ) − ( n − 1 ) . n . ( n + 1 ) 3 A = n . ( n + 1 ) . ( n + 2 ) A = [ n . ( n + 1 ) . ( n + 2 ) ] : 3 S = [ n . ( n + 1 ) . ( n + 2 ) ] : 3 + 2. ( 1 + 2 + 3 + . . . + n ) S = [ n . ( n + 1 ) . ( n + 2 ) ] : 3 + 2. n . ( n + 1 ) : 2 S = n . ( n + 1 ) . ( n + 2 ) : 3 + n . ( n + 1 ) S = n . ( n + 1 ) . [ ( n + 2 ) : 3 + 1 )
D = 1^2 + 2^2 + 3^2 + ... + n^2
= 1.( 2 - 1 ) + 2.( 3-1 ) + 3.( 4-1 ) + .... + n.[ ( n+ 1) - 1 ]
= 1.2 - 1 + 2.3 - 2 + 3.4 - 3 + .... + n.( n+1 ) - n
= [ 1.2 + 2.3 + 3.4 + ..... + n.( n + 1 ) ] - ( 1 + 2 + 3 + .... + n )
= { [ n.( n+1 ).( n+2 )] /3 } - { [ n.( n+1)] /2 }
= { n(n+1)(2n+1) }/ 6
Vậy.........
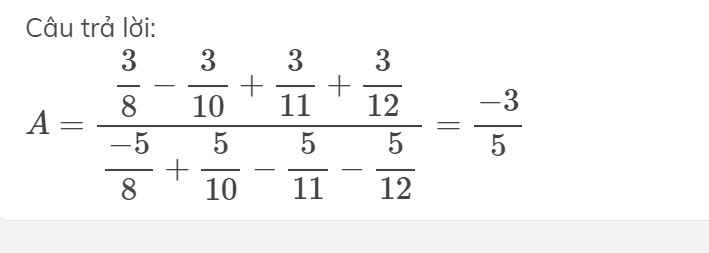
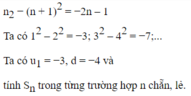
A = 1 + (1+ 1).2 + (1 + 2).3 + (1+3).4 + ...+ (1 + n-1). n
A = 1 + (2+1.2) + (3+ 2.3) + (4 + 3.4) + ....+ ( n + (n -1).n)
A = (1+ 2 + 3 + 4 + ...+ n) + (1.2 + 2.3 + 3.4 + .....+ (n-1).n)
Tính B = 1+ 2+ 3 + ...+ n = (n +1).n/ 2
C = 1.2+ 2.3 + 3.4 + ...+ (n-1).n
=> 3.C = 1.2.3 + 2.3.3 + 3.4.3 + ...+ (n-1).n.3
3C = 1.2.3 + 2.3. (4 -1) + 3.4.(5 - 2) + ... + (n -1).n [(n+ 1) - (n -2)]
3C = [1.2.3 + 2.3.4 + ....+ (n-1).n.(n +1)] - (1.2.3 + 2.3.4 + ... + (n-2)(n -1).n)
3C = (n -1).n (n +1) => C = (n -1).n.(n +1)/ 3
Vậy A = (n +1).n/ 2 + (n -1).n(n +1)/3