Tính giá trị của biểu thức: C= \(5\cos^2a+2\sin^2a.Biết\sin a=\frac{2}{3}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(A = \frac{{\sin \frac{\pi }{{15}}\cos \frac{\pi }{{10}} + \sin \frac{\pi }{{10}}\cos \frac{\pi }{{15}}}}{{\cos \frac{{2\pi }}{{15}}\cos \frac{\pi }{5} - \sin \frac{{2\pi }}{{15}}\sin \frac{\pi }{5}}} = \frac{{\sin \left( {\frac{\pi }{{15}} + \frac{\pi }{{10}}} \right)}}{{\cos \left( {\frac{{2\pi }}{{15}} + \frac{\pi }{5}} \right)}} = \frac{{\sin \frac{\pi }{6}}}{{\cos \frac{\pi }{3}}} = 1\)
b) \(B = \sin \frac{\pi }{{32}}\cos \frac{\pi }{{32}}\cos \frac{\pi }{{16}}\cos \frac{\pi }{8} = \frac{1}{2}\sin \frac{\pi }{{16}}.\cos \frac{\pi }{{16}}.\cos \frac{\pi }{8} = \frac{1}{4}\sin \frac{\pi }{8}.\cos \frac{\pi }{8} = \frac{1}{8}\sin \frac{\pi }{4} = \frac{1}{8}.\frac{{\sqrt 2 }}{2} = \frac{{\sqrt 2 }}{{16}}\;.\)

\(1+tan^2a=\frac{1}{cos^2a}\)
\(1+3^2=\frac{1}{cos^2a}\)
\(10=\frac{1}{cos^2a}\)
\(cos^2a=\frac{1}{10}\)
\(cosa=\pm\sqrt{\frac{1}{10}}\)
\(sin^2a+cos^2a=1\)
\(sin^2a+\frac{1}{10}=1\)
\(sin^2a=\frac{9}{10}\)
\(sina=+\sqrt{\frac{9}{10}}\)
Vì tan dương nên có hai trường hợp :
TH1 : cả sin và cos cùng dương :
\(A=\frac{sina\cdot cosa}{sin^2a-cos^2a}\)
\(=\frac{\sqrt{\frac{9}{10}}\cdot\sqrt{\frac{1}{10}}}{\frac{9}{10}-\frac{1}{10}}\)
\(=\frac{\frac{3}{10}}{\frac{8}{10}}\)
\(=\frac{3}{8}\)
TH2 : cả sin và cos cùng âm
\(A=\frac{sina\cdot cosa}{sin^2a-cos^2a}\)
\(=\frac{-\sqrt{\frac{9}{10}}\cdot-\sqrt{\frac{1}{10}}}{\frac{9}{10}-\frac{1}{10}}\)
\(=\frac{\frac{3}{10}}{\frac{8}{10}}\)
\(=\frac{3}{8}\)

Chọn A.
Áp dụng công thức biến đổi tổng thành tích và công thức nhân đôi; ta có
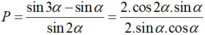


Ta có: \(A = 2{\sin ^2}\alpha + 5{\cos ^2}\alpha = 2({\sin ^2}\alpha + {\cos ^2}\alpha ) + 3{\cos ^2}\alpha \)
Mà \({\cos ^2}\alpha + {\sin ^2}\alpha = 1;\cos \alpha = - \frac{{\sqrt 2 }}{2}.\)
\( \Rightarrow A = 2 + 3.{\left( { - \frac{{\sqrt 2 }}{2}} \right)^2} = 2 + 3.\frac{1}{2} = \frac{7}{2}.\)

Lời giải:
\(M=\frac{\frac{\sin a}{\cos a}+1}{\frac{\sin a}{\cos a}-1}=\frac{\tan a+1}{\tan a-1}=\frac{\frac{3}{5}+1}{\frac{3}{5}-1}=-4\)
\(N = \frac{\frac{\sin a\cos a}{\cos ^2a}}{\frac{\sin ^2a-\cos ^2a}{\cos ^2a}}=\frac{\frac{\sin a}{\cos a}}{(\frac{\sin a}{\cos a})^2-1}=\frac{\tan a}{\tan ^2a-1}=\frac{\frac{3}{5}}{\frac{3^2}{5^2}-1}=\frac{-15}{16}\)

a) \(M = \sin {45^o}.\cos {45^o} + \sin {30^o}\)
Ta có: \(\left\{ \begin{array}{l}\sin {45^o} = \cos {45^o} = \frac{{\sqrt 2 }}{2};\;\\\sin {30^o} = \frac{1}{2}\end{array} \right.\)
Thay vào M, ta được: \(M = \frac{{\sqrt 2 }}{2}.\frac{{\sqrt 2 }}{2} + \frac{1}{2} = \frac{2}{4} + \frac{1}{2} = 1\)
b) \(N = \sin {60^o}.\cos {30^o} + \frac{1}{2}.\sin {45^o}.\cos {45^o}\)
Ta có: \(\sin {60^o} = \frac{{\sqrt 3 }}{2};\;\;\cos {30^o} = \frac{{\sqrt 3 }}{2};\;\sin {45^o} = \frac{{\sqrt 2 }}{2};\, \cos {45^o}= \frac{{\sqrt 2 }}{2}\)
Thay vào N, ta được: \(N = \frac{{\sqrt 3 }}{2}.\frac{{\sqrt 3 }}{2} + \frac{1}{2}.\frac{{\sqrt 2 }}{2}.\frac{{\sqrt 2 }}{2} = \frac{3}{4} + \frac{1}{4} = 1\)
c) \(P = 1 + {\tan ^2}{60^o}\)
Ta có: \(\tan {60^o} = \sqrt 3 \)
Thay vào P, ta được: \(Q = 1 + {\left( {\sqrt 3 } \right)^2} = 4.\)
d) \(Q = \frac{1}{{{{\sin }^2}{{120}^o}}} - {\cot ^2}{120^o}.\)
Ta có: \(\sin {120^o} = \frac{{\sqrt 3 }}{2};\;\;\cot {120^o} = \frac{{ - 1}}{{\sqrt 3 }}\)
Thay vào P, ta được: \(Q = \frac{1}{{{{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2}}} - \;{\left( {\frac{{ - 1}}{{\sqrt 3 }}} \right)^2} = \frac{1}{{\frac{3}{4}}} - \;\frac{1}{3} = \;\frac{4}{3} - \;\frac{1}{3} = 1.\)
ta có sin a^2=4/9 =>cos a^2=1-4/9=5/9
C=5*5/9+2*4/9+11/3