Tìm cực trị của hàm số y=-x³+3x²+2. Hàm số có 2 cực trị AB. Tìm trung điểm AB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LV
0
CM
19 tháng 7 2018
Ta có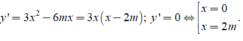 
Đề đồ thị hàm số có hai điểm cực trị khi m khác 0.
Khi đó tọa độ hai điểm cực trị là A( 0 ; 4m2- 2) và B( 2m; 4m2- 4m3-2).
Do I( 1; 0) là trung điểm của AB nên
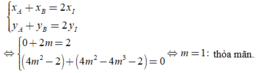
Chọn C.
23 tháng 4 2016
Ta có : \(y'=3x^2-6x+m^2\Rightarrow y'=0\Leftrightarrow3x^2-6x+m^2=0\left(1\right)\)
Hàm số có cực trị \(\Leftrightarrow\left(1\right)\) có 2 nghiệm phân biệt \(x_1;x_2\)
\(\Leftrightarrow\Delta'=3\left(3-m^2\right)>0\Leftrightarrow-\sqrt{3}< m< \sqrt{3}\)
Phương trình đường thẳng d' đi qua các điểm cực trị là : \(y=\left(\frac{2}{3}m^2-2\right)x+\frac{1}{3}m^2\)
=> Các điểm cực trị là :
\(A\left(x_1;\left(\frac{2}{3}m^2-2\right)x_1+\frac{1}{3}m^2+3m\right);B\left(x_2;\left(\frac{2}{3}m^2-2\right)x_2+\frac{1}{3}m^2+3m\right);\)
Gọi I là giao điểm của hai đường thẳng d và d' :
\(\Rightarrow I\left(\frac{2m^2+6m+15}{15-4m^2};\frac{11m^2+3m-30}{15-4m^2}\right)\)
A và B đối xứng đi qua d thì trước hết \(d\perp d'\Leftrightarrow\frac{2}{3}m^2-2=-2\Leftrightarrow m=0\)
Khi đó \(I\left(1;-2\right);A\left(x_1;-2x_1\right);B\left(x_2;-2x_2\right)\Rightarrow I\) là trung điểm của AB=> A và B đối xứng nhau qua d
Vậy m = 0 là giá trị cần tìm
CM
5 tháng 10 2017
Chọn D
Ta có y ' = 3 x 2 - 6 m x + m - 1
Hàm số có cực đại, cực tiểu khi và chỉ khi PT y ' = 0 có hai nghiệm phân biệt
Điều này tương đương
Hai điểm cực trị có hoành độ dương
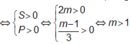
Vậy các giá trị cần tìm của m là m >1
CM
8 tháng 10 2017
Ta có
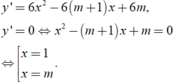
Để hàm số có hai điểm cực trị khi m khác -1
Tọa độ các điểm cực trị là A( 1; m3+ 3m-1) và B( m; 3m2)
Suy ra
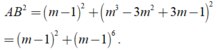
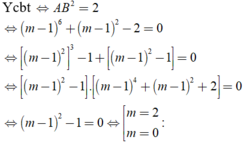
Chọn B.
\(y'=-3x^2+6x=0\Rightarrow\left\{{}\begin{matrix}x=0\Rightarrow y=2\\x=2\Rightarrow y=6\end{matrix}\right.\)
\(\Rightarrow A\left(0;2\right)\) ; \(B\left(2;6\right)\)
Theo công thức trung điểm ta có tọa độ trung điểm AB là \(\left(1;4\right)\)