Cho 100 đường thẳng phân biệt trong đó không có hai đường thẳng nào song song với nhau. Hỏi chúng cắt nhau bao nhiêu điểm nếu:
a) Không có 3 đường thẳng nào đồng quy
b) Có đúng 5 đường thẳng đồng quy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 7 2023
Số giao điểm tất cả là:
\(C^2_{100}\left(giao\right)\)
CM
5 tháng 2 2018
Đáp án C
2. Nếu 3 mặt phẳng đôi một cắt nhau theo 3 giao tuyến phân biệt thì 3 giao tuyến ấy hoặc đồng quy, hoặc đôi một song song với nhau
8. Cho 2 đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia
5 tháng 3 2022
Áp dụng công thức tìm số đường thẳng phân biệt khi biết số giao điểm, gọi số giao điểm là n, ta có:
Số đường thẳng phân biệt tạo được\(=1+...+\left(n-1\right)\)
Vậy từ bài toán ta được: \(1+2+...+\left(n-1\right)=8\)
\(\Rightarrow\left[1+\left(n-1\right)\right]\cdot\frac{\left(n-1\right)}{2}=8\)
\(\Rightarrow\left(1+n-1\right)\left(n-1\right):2=8\)
\(\Rightarrow n\cdot\left(n-1\right):2=8\)
\(\Rightarrow n\cdot\left(n-1\right)=16\)
26 tháng 8 2017
a ) Số giao điểm của chúng là :
11 x 10 : 2 = 55 ( giao điểm )
b ) Giả sử trong 11 đường thẳng đó ko có 3 đg thẳng nào đồng quy thì số giao điểm là : 11 x 10 : 2 = 55 ( giao điểm )
Do ko có 3 đường thẳng nào đồng quy nên số giao điểm đc tạo bởi 5 đg thẳng là : 5 x 4 : 2 = 10 ( giao điểm )
Trên thực tế , 5 đg thẳng đó đồng quy nên số giao điểm mà chúng tạo đc là 1 giao điểm .
Suy ra số giao điểm thỏa mãn đề bài là : 55 - 10 + 1 = 46 ( giao điểm )
a ) Bài toán tổng quát :
Cho n đường thẳng trong đó ko có 3 đường thẳng nào đồng quy thì số giao điểm là : n . ( n - 1 ) : 2 giao điểm
b ) Bài toán tổng quát :
Cho n đường thẳng trong đó có m đường thẳng đồng quy thì số giao điểm là :
n . ( n - 1 ) : 2 - m . ( m - 1 ) : 2 + 1 giao điểm
B1
12 tháng 9 2017
đề sai
Cho 6 đường thẳng đôi một cắt nhau trong đó không có ba đường thẳng nào đồng quy. Tính số giao điểm của chúng.
Bài làm
Lời giải:
Ta thấy cứ một đường thẳng trong 6 đường thẳng đã cho cắt 5 đường thẳng còn lại tạo thành 5 giao điểm.
Vì có 6 đường thẳng nên số giao điểm sẽ là : 6.5 = 30 ( giao điểm)
Nhưng mỗi giao điểm đã được tính 2 lần nên số giao điểm thực tế là : 30:2 = 15 giao điểm.
Nhận xét : Bài toán này em có thể tổng quát như sau :
Cho n đường thẳng (n>1, n là số tự nhiên ) đôi một cắt nhau trong đó không có ba đường thẳng nào đồng quy. Thì số giao điểm tạo thành là :
Ví dụ n = 100 thì số giao điểm sẽ là : (100.99) :2=4950 ( giao điểm)
Hướng dẫn thêm: Đây là bài toán ở mức độ Khá. Để làm tốt các bài toán tương tự, em nên ôn luyện thêm tại đây: Chuyên đề - Điểm và đường thẳng (Nâng cao)
Chúc em học tốt, thân!
CM
11 tháng 9 2019
a) Vẽ hình
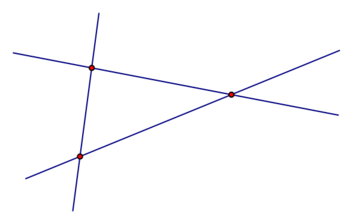
b) Từng cặp đường thẳng cắt nhau tạo ra 3 giao điểm.
ban thong cam minh chua nghi ra cau b
cau a chung cat nhau 4950 diem