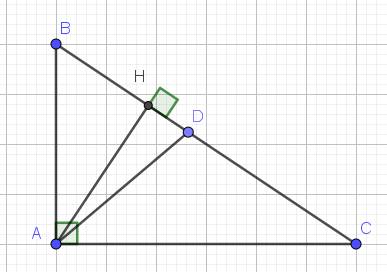
cho tam giác abc vuong tại a,đường cao ah.biết ab=7,ac=9.tính ah,hc,bc.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
L
Luyến
11 tháng 7 2021
Ngu dốt
Đúng(0)
Những câu hỏi liên quan
21 tháng 7 2017
A B C H
ta co \(AH^2=BH\cdot HC\Rightarrow AH^2=1,8HC\)
ap dung dl pitago vao tam giac vuong AHC co \(AH^2+CH^2=AC^2\Rightarrow1,8HC+HC^2=16\)
\(\Rightarrow CH^2+1,8CH-16=0\Rightarrow\left(CH-3,2\right)\left(CH+5\right)=0\)
\(\Rightarrow CH=3,2\) (do BH>0)
\(\Rightarrow AH^2=1,8\cdot CH=5.76\Rightarrow AH=2,4\)
\(BH+HC=BC\Rightarrow BC=1,8+3,2=5\)
ap dung dl pitago ta tinh dc \(AB^2+AC^2=BC^2\Rightarrow AB=3\)
NV
25 tháng 6 2016
Đặt BH = x (x > 0) => BC = (x + 6,4)
Có: AB2 = BH.BC => 36 = x(x + 6,4) => 36 = x2 + 6,4x => x2 + 6,4x - 36 = 0
=> (x + 10)(5x - 18) = 0 => x = -10 (loại) hoặc x = 18/5 (nhận)
=> BH = 18/5cm => BC = 18/5 + 6,4 = 10cm
Có: AC2 = HC.BC = 6,4 . 10 = 64 => AC = 8cm
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{6^2}+\frac{1}{8^2}=\frac{25}{576}\Rightarrow AH=\sqrt{\frac{576}{25}}=\frac{24}{5}cm\)
Vậy BC = 10cm , BH = 18/5cm , AH = 24/5cm , AC = 8cm
26 tháng 6 2016
\(\Delta ABC\)có A=90 và AH là đường cao
Áp dụng hệ thức giữa cạnh góc vuông và hingf chiếu của nó trên cạnh huyền
=> \(AB^2=CH.BC\); \(AC^2=HC.BC\)
<=> \(AB^2=\left(BC-CH\right)BC\)
<=>\(BC^2=AB^2+CH.BH\)
=>\(BC^2=6^2+6,4.BC\)
<=> \(BC^2-6,4.BC-36=0\)
=> BC = 10(cm) (nhận) : BC=- 3,6 (cm) (loại)
=> \(AC=\sqrt{CH.BC}=\sqrt{6,4.10}=8\)(cm)
=>BH= BC - CH =10 - 6,4 = 3,6 (cm)
Áp dụng hệ thức giữa đường cao và các cạnh trong tam giác
=> AH.BC =AB.AC
=>AH = \(\frac{AB.AC}{BC}=\frac{6.8}{10}=4.8\left(cm\right)\)
Vậy AH =4,8 (cm) ; BC = 10 (cm) ; AC =8(cm) ; BH = 3,6 (cm)
H
2
30 tháng 8 2018
Cho tam giác ABC vuông tại A, AH là đường cao. Biết AB=15cm,HC=16cm.Tính BC,AH,HB,AC.
AH
Akai Haruma
Giáo viên
13 tháng 1 2024
Lời giải:
a. Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{12^2+16^2}=20$ (cm)
Áp dụng tính chất đường phân giác:
$\frac{BD}{DC}=\frac{AB}{AC}=\frac{12}{16}=\frac{3}{4}$
Mà: $BD+DC=BC=20$ nên:
$BD=20:(3+4).3=\frac{60}{7}$ (cm)
$CD= 20:(3+4).4=\frac{80}{7}$ (cm)
b.
$AH=2S_{ABC}:BC=\frac{AB.AC}{BC}=\frac{12.16}{20}=9,6$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{12^2-9,6^2}=7,2$ (cm)
$HD = BD-BH = \frac{60}{7}-7,2=\frac{48}{35}$ (cm)
$AD = \sqrt{AH^2+HD^2}=\sqrt{9,6^2+(\frac{48}{35})^2}=\frac{48\sqrt{2}}{7}$ (cm)
