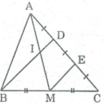
cho tam giác abc, d là điểm thuộc cạnh ac sao cho ad=1/2 dc. gọi m là trung điểm của bc, e là giao điểm của bd và am. Chứng minh ae=em.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 1 2017
Gọi E là trung điểm của DC
Trong ΔBDC, ta có:
M là trung điểm của BC (gt)
E là trung điểm của CD (gt)
Nên ME là đường trung bình của ∆ BCD
⇒ME // BD (tính chất đường trung bình tam giác)
Suy ra: DI // ME
AD = 1/2 DC (gt)
DE = 1/2 DC (cách vẽ)
⇒ AD = DE và DI//ME
Nên AI= IM (tính chất đường trung bình của tam giác).
5 tháng 8 2021
Gọi K là trung điểm của DC
Suy ra: AD=DK=KC
Xét ΔBDC có
M là trung điểm của BC
K là trung điểm của DC
Do đó: MK là đường trung bình của ΔBDC
Suy ra: MK//BD và \(MK=\dfrac{BD}{2}\)
hay ID//MK
Xét ΔAMK có
D là trung điểm của AK
DI//MK
Do đó: I là trung điểm của AM
hay IA=IM
30 tháng 6 2018
Lấy N là trung điểm của DC ; ta có \(AD=DN=NC\)
Xét tam giác BCD có MN là đường trung bình \(\Rightarrow MN\text{//}BD\) hay \(MN\text{//}ID\)
Xét tam giác AMN có D là trung điểm của AN; ID//MN (cmt) => I là trung điểm của AM
=> ĐPCM
25 tháng 6 2016
bài 1 làm sao vậy sao ko thấy mấy câu trả lời vậy bạn giúp mình giải bài tập số 1 với cảm ơn nhiều
VT
10 tháng 7 2018
Cho tam giác ABC ,điểm D thuộc cạnh AC sao cho AD = \(\frac{1}{2}\)DC .Gọi M là trung điểm của BC ,Ilaf giao điểm của AM và BD .Chứng minh rằng : IA=IM
Lấy E là trung điểm của DC
=> AD = DE = EC
Xét \(\Delta AEM\) có ME là trung bình:
=> \(ME//BD\left(ME//ID\right)\)
Xét \(\Delta AME\)có D là trung điểm của AE;ME//ID
=> I là trung điểm của AM
=>IA=IM (đpcm)
HN
10 tháng 7 2018
Lấy E là trung điểm của DC
\(\Rightarrow AD=DE=EC\)
Xét \(\Delta BCD\)có ME là trung bình:
\(\Rightarrow ME//BD\left(ME//ID\right)\)
Xét \(\Delta AME\)có D là trung điểm của \(AE\); \(ME//ID\)( cmt )
\(\Rightarrow I\)là trung điểm của AM
\(\Rightarrow IA=IM\left(đpcm\right)\)
G
21 tháng 7 2019
Hình bạn tự vẽ nhé
Giải: Kẻ \(MG//BD\) ta có: \(\hept{\begin{cases}MG//BD\\MB=MC\left(gt\right)\end{cases}}\Rightarrow\) MG là đường trung bình tam giác BCD.
\(\Rightarrow DG=CG=\frac{1}{2}CD\Rightarrow DG=AD\)
Xét tam giác AMG ta có: \(\hept{\begin{cases}MG//DI\\AD=DG\end{cases}}\Rightarrow AI=IM\left(đpcm\right)\) (tc đường tb tam giác)