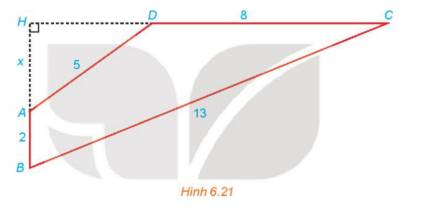
Cho tứ giác ABCD có AB vuông góc với CD và AB = 2, BC = 13,CD = 8,DA = 5. Tính diện tích tứ giác ABCD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
30 tháng 9 2023
Ta có :AH=x (x>0)
Xét tam giác AHD vuông ở H, ta có:
\(A{D^2} = A{H^2} + H{D^2} \Leftrightarrow H{D^2} = A{D^2} - A{H^2} = 25 - {x^2}\)
\( \Rightarrow HD = \sqrt {25 - {x^2}} \)
Ta có: \(HC = HD + DC = \sqrt {25 - {x^2}} + 8\)
\(HB = AH + AB = x + 2\)
Xét tam giác HBC vuông tại H, ta có:
\(\begin{array}{l}B{C^2} = H{B^2} + H{C^2}\\ \Leftrightarrow {13^2} = {(x + 2)^2} + {\left( {\sqrt {25 - {x^2}} + 8} \right)^2}\\ \Leftrightarrow 169 = {x^2} + 4x + 4 + 25 - {x^2} + 16\sqrt {25 - {x^2}} + 64\\ \Leftrightarrow 16\sqrt {25 - {x^2}} = - 4x + 76\\ \Leftrightarrow 4\sqrt {25 - {x^2}} = - x + 19\end{array}\)
Bình phương hai vế của phương trình trên ta được:
\(\begin{array}{l}16(25 - {x^2}) = {x^2} - 38x + 361\\ \Leftrightarrow 17{x^2} - 38x - 39 = 0\end{array}\)
\( \Leftrightarrow x = 3\) hoặc \(x = \frac{{ - 13}}{{17}}\)
Thay lần lượt các giá trị trên vào phương trình, ta thấy hai giá trị đều thỏa mãn
Do x>0 nên ta chọn x = 3 => AH = 3
\(\begin{array}{l}HD = \sqrt {25 - {3^2}} = 4\\HC = 4 + 8 = 12\\HB = 3 + 2 = 5\end{array}\)
Diện tích tam giác HAD là \({S_1} = \frac{1}{2}.HA.HD = \frac{1}{2}.3.4 = 6\)
Diện tích tam giác HBC là \({S_2} = \frac{1}{2}.HB.HC = \frac{1}{2}.5.12 = 30\)
Vậy diện tích tứ giác ABCD là \(S = {S_2} - {S_1} = 30 - 6 = 24\)
CM
12 tháng 12 2018
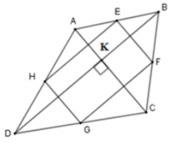
Vì E, F, G, H lần lượt là trung điểm các cạnh AB,BC,CD,DA nên EF, FG, GH, HE lần lượt là đường trung bình của tam giác ABC, BCD, ADC, ADB nên
EF//HG (cùng song song với AC)
HE//FG (cùng song song với BD)
Suy ra tứ giác EFGH là hình bình hành
Mà A C ⊥ B D (gt) ⇒ E F ⊥ F G
Suy ra EFGH là hình chữ nhật
Do đó S E F G H = H E . E F mà E F = 1 2 A C ; H E = 1 2 B D (tính chất đường trung bình)
CM
17 tháng 3 2017
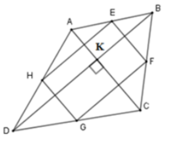
Vì E, F, G, H lần lượt là trung điểm các cạnh AB,BC,CD,DA nên EF, FG, GH, HE lần lượt là đường trung bình của tam giác ABC, BCD, ADC, ADB nên
EF//HG (cùng song song với AC)
HE//FG (cùng song song với BD)
Suy ra tứ giác EFGH là hình bình hành
Mà A C ⊥ B D (gt) ⇒ E F ⊥ F G
Suy ra EFGH là hình chữ nhật
Do đó S E F G H = H E . E F mà E F = 1 2 A C ; H E = 1 2 B D (tính chất đường trung bình)
Đáp án D
3 tháng 4 2023
AB=BM
nên \(S_{QAB}=S_{QBM}\)
DA=AQ
=>\(S_{BDA}=S_{BAQ}\)
=>\(S_{QAM}=2\cdot S_{ABD}\)
Tương tự, ta được: \(S_{MBN}=2\cdot S_{ABC};S_{NCP}=2\cdot S_{BCD};S_{PDQ}=2\cdot S_{ADC}\)
=>\(S_{MNPQ}=5\cdot S_{ABCD}=300\left(cm^2\right)\)
4 tháng 12 2023
1: Xét ΔCAB có
F,E lần lượt là trung điểm của CA,CB
=>FE là đường trung bình của ΔCAB
=>FE//AB và \(FE=\dfrac{AB}{2}\)
Xét ΔDAB có
G,H lần lượt là trung điểm của DA,DB
=>GH là đường trung bình của ΔDAB
=>GH//AB và \(GH=\dfrac{AB}{2}\)
GH//AB
FE//AB
Do đó: GH//FE
Ta có: \(GH=\dfrac{AB}{2}\)
\(FE=\dfrac{AB}{2}\)
Do đó: GH=FE
Xét tứ giác EFGH có
GH=FE
GH//FE
Do đó: EFGH là hình bình hành
2: AB=CD
mà AB=8cm
nên CD=8cm
Xét ΔADC có
G,F lần lượt là trung điểm của AD,AC
=>GF là đường trung bình của ΔADC
=>GF//DC và \(GF=\dfrac{DC}{2}=4cm\)
GF//DC
DC\(\perp\)AB
Do đó: GF\(\perp\)AB
Ta có: GF\(\perp\)AB
AB//GH
Do đó: GH\(\perp\)GF
Xét hình bình hành GHEF có GH\(\perp\)GF
nên GHEF là hình chữ nhật
=>\(S_{GHEF}=GH\cdot GF=\dfrac{AB}{2}\cdot\dfrac{CD}{2}=4\cdot4=16\left(cm^2\right)\)
Bạn xem hình vẽ ở đây nhé: https://i.imgur.com/sh8KysD.png
Gọi CD giao AB tại O, Đặt OD=a, OA=b.
Xét tam giác OAD vuông tại O ta có
a^2 + b^2 =25
Xét tam giác OBC vuông tại O ta có
(a+8^2 )+ (b+2^2=13^2
Từ đó tính được a=84/17 hoặc a=4. Loại a=84/17vì với a=84/17 thì b<0
Với a=4 suy ra b=3. Khi đó SABCD=SOBC-SOAD=24
Bạn xem hình vẽ ở đây nhé: https://i.imgur.com/sh8KysD.png
Gọi CD giao AB tại O, Đặt OD=a, OA=b.
Xét tam giác OAD vuông tại O ta có \(a^2+b^2=25\)
Xét tam giác OBC vuông tại O ta có \(\left(a+8\right)^2+\left(b+2\right)^2=13^2\)
Từ đó tính được a \(=\frac{87}{17}\)hoặc a = 4. Loại a = \(\frac{87}{17}\)vì với a = \(\frac{87}{17}\) thì \(b< 0\)
Với a = 4 suy ra b = 3. Khi đó \(^SABCD=^SOBC-^SOAD=24\)