Giải giúp mình bài này
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(R_{tđ}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{24\cdot12}{24+12}=8\Omega\)
\(I=\dfrac{U}{R}=\dfrac{12}{8}=1,5A\)
\(P=\dfrac{U^2}{R}=\dfrac{12^2}{8}=18W\)
\(Q_{tỏa1}=A_1=U_1\cdot I_1\cdot t=12\cdot\dfrac{12}{24}\cdot1\cdot3600=21600J\)
\(Q_{tỏa2}=A_2=U_2\cdot I_2\cdot t=12\cdot\dfrac{12}{12}\cdot1\cdot3600=43200J\)



Sau khi phơi còn lại số thóc là:
780 – 130 = 650 (kg)`
Lượng nước trong 650 kg thóc tươi là:
650 : 100 × 25 = 162,5 (kg)`
Lượng thóc thuần hạt trong 650 kg thóc tươi là:
650 – 162,5 = 487,5 (kg)
Lượng nước còn lại trong thóc sau khi phơi là:
650 – 487,5 = 162,5 (kg)
Tỉ số % giữa lượng nước và lượng thuần hạt có trong thóc đã phơi là:
162,5 : 487,5 × 100 = 33,33%
Đáp số: 33,33%

e: \(=\dfrac{-3}{4}+\dfrac{5}{7}=\dfrac{-21+20}{28}=\dfrac{-1}{28}\)
a ) \(\dfrac{6}{13}\) + \(\dfrac{-14}{39}\)
= \(\dfrac{6.3}{13.3}\) + \(\dfrac{-14}{39}\)
= \(\dfrac{18}{39}\) - \(\dfrac{14}{39}\)
= \(\dfrac{4}{39}\)
{ các ý còn lại tương tự }


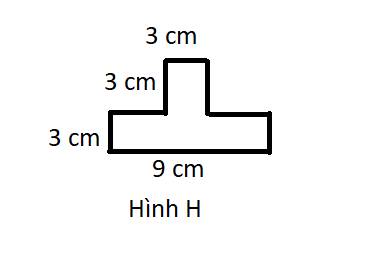 Các bạn giúp mình giải bài này bằng bài giải nha !
Các bạn giúp mình giải bài này bằng bài giải nha ! 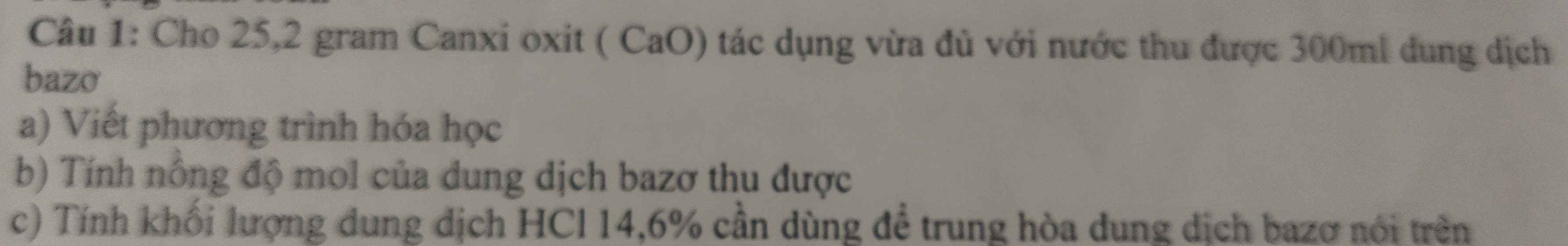





a) Âp dụng định lý Py-ta-go trong\(\Delta ABC\) vuông tại A có đường cao AH:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AB+\sqrt{BC^2-AC^2}=\sqrt{29^2-20^2}=\sqrt{441}=21\left(cm\right)\)
Áp dụng hệ thức lượng cho \(\Delta ABC\) vuông tại A có đường cao AH
\(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{21.20}{29}=\dfrac{420}{29}\left(cm\right)\)
b)\(AC^2=CH.CB\Rightarrow CH=\dfrac{AC^2}{CB}=\dfrac{20^2}{29}=\dfrac{400}{29}\left(cm\right)\)
xét tam giác AHC có AD là Phân giác của \(\widehat{HAC}\) ta có:
\(\dfrac{DC}{DH}=\dfrac{AC}{AH}\Leftrightarrow\dfrac{DC}{AC}=\dfrac{DH}{AH}=\dfrac{DC+DH}{AC+AH}=\dfrac{CH}{AC+AH}=\dfrac{400}{\dfrac{29}{20+\dfrac{420}{29}}}=\dfrac{2}{5}\)
\(\Rightarrow DC=\dfrac{2}{5}AC=\dfrac{2}{5}20=8\left(cm\right)\)
\(S_{ADC}=\dfrac{CD.AH}{2}=\dfrac{8.\dfrac{420}{29}}{2}=\dfrac{2680}{2}\left(cm^2\right)\)
\(S_{ADC}=\dfrac{1680}{2}\left(cm^2\right)\)