ABC vuông tại A, vẽ AH vuông góc BC (H thuộc BC). CMR 2AH2+BH2+CH2=BC2Giúp mình với ạ❕Mình cần...
Đọc tiếp
ABC vuông tại A, vẽ AH vuông góc BC (H thuộc BC). CMR 2AH2+BH2+CH2=BC2
Giúp mình với ạ❕Mình cần gấp❕
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
K
1
Những câu hỏi liên quan
31 tháng 7 2023
\(AB^2=AH^2+BH^2\Rightarrow AH^2=AB^2-BH^2\left(1\right)\left(Pitago\right)\)
\(AC^2=AH^2+CH^2\Rightarrow AH^2=AC^2-CH^2\left(2\right)\left(Pitago\right)\)
\(\left(1\right),\left(2\right)\Rightarrow AC^2-CH^2=AB^2-BH^2\)
\(\Rightarrow AB^2+CH^2=AC^2+BH^2\)
\(\Rightarrow dpcm\)
31 tháng 7 2023
Ta có \(AB^2-AC^2=\left(BH^2+AH^2\right)-\left(CH^2+AH^2\right)\) \(=BH^2-CH^2\) \(\Rightarrow AB^2+CH^2=AC^2+BH^2\), đpcm.
(Bài này kết quả vẫn đúng nếu không có điều kiện tam giác ABC vuông tại A.)
23 tháng 11 2023
ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ACB}+40^0=90^0\)
=>\(\widehat{ACB}=90^0-40^0=50^0\)
ΔBAH vuông tại H
=>\(\widehat{BAH}+\widehat{B}=90^0\)
=>\(\widehat{BAH}=90^0-40^0=50^0\)
ΔCAH vuông tại H
=>\(\widehat{HAC}+\widehat{C}=90^0\)
=>\(\widehat{HAC}=90^0-\widehat{C}=90^0-50^0=40^0\)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
1 tháng 8 2023
a/
\(BC=\sqrt{AB^2+AC^2}\) (Pitago)
\(\Rightarrow BC=\sqrt{10^2+15^2}=\sqrt{325}=5\sqrt{13}\)
\(AB^2=HB.BC\) (Trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
\(\Rightarrow HB=\dfrac{AB^2}{BC}=\dfrac{10^2}{5\sqrt{13}}=\dfrac{20\sqrt{13}}{13}\)
\(HC=BC-HB=5\sqrt{13}-\dfrac{20\sqrt{13}}{13}\)
\(AH^2=HB.HC\) (trong tg vuông bình phương đường cao hạ từ đỉnh góc vuông xuống cạnh huyền bằng tích giữa 2 hình chiếu của 2 cạnh góc vuông trên cạnh huyền)
Bạn tự thay số tính nốt nhé vì số hơi lẻ
b/
Áp dụng tính chất đường phân giác trong tg: đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề của hai đoạn thẳng ấy
\(\Rightarrow\dfrac{IA}{IC}=\dfrac{AB}{BC}=\dfrac{10}{5\sqrt{13}}=\dfrac{2\sqrt{13}}{13}\)
Mà \(IA+IC=AC=15\) Từ đó tính được IA và IC
Xét tg vuông ABI có
\(BI=\sqrt{AB^2+IA^2}\) (pitago)
Bạn tự thay số tính nhé
26 tháng 11 2023
a: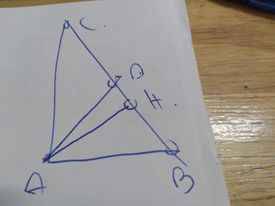 
b: AD là phân giác của góc BAC
=>\(\widehat{BAD}=\widehat{CAD}=\dfrac{1}{2}\cdot\widehat{BAC}=\dfrac{1}{2}\cdot90^0=45^0\)
Xét ΔADC có \(\widehat{ADH}\) là góc ngoài tại đỉnh D
nên \(\widehat{ADH}=\widehat{DAC}+\widehat{DCA}\)
=>\(\widehat{ADH}=45^0+30^0=75^0\)
b: ΔHAD vuông tại H
=>\(\widehat{HAD}+\widehat{HDA}=90^0\)
=>\(\widehat{HAD}+75^0=90^0\)
=>\(\widehat{HAD}=15^0\)
Vì \(\widehat{DAH}< \widehat{DAB}\)
nên AH nằm giữa AD và AB
=>\(\widehat{DAH}+\widehat{BAH}=\widehat{BAD}\)
=>\(\widehat{BAH}+15^0=45^0\)
=>\(\widehat{BAH}=30^0>\widehat{HAD}\)
d: \(\widehat{ABC}+\widehat{ACB}=90^0\)(ΔABC vuông tại A)
\(\widehat{HAC}+\widehat{C}=90^0\)(ΔAHC vuông tại H)
Do đó: \(\widehat{ABC}=\widehat{HAC}\)
26 tháng 11 2023
`a)`
`b)`
Có `Delta ABC` vuông tại `A` có `hat(C)=30^0`
`=>hat(B)=60^0`
`AD` là phân giác `hat(BAC)=>hat(BAD)=hat(A_3)=1/2hat(BAC)`
`=>hat(BAD)=hat(A_3)=1/2*90^0=45^0`
`Delta BAD` có `hat(B)+hat(D_1)+hat(BAD)=180^0`
hay `60^0+hat(D_1)+45^0=180^0`
`=>hat(D_1)=180^0-60^0-45^0=75^0`
`c)`
Có `Delta AHD` vuông tại `H(AH⊥BC)` có `hat(D_1)=75^0`
`=>hat(A_1)=15^0`
Có `hat(A_1)+hat(A_2)=hat(BAD)`
hay`15^0+hat(A_2)=45^0`
`=>hat(A_2)=30^0`
Có `15^0<30^0`
`=>hat(A_1)<hat(A_2)`
`d)`
Có `hat(A_1)+hat(A_3)=hat(HAC)`
hay `15^0+45^0=hat(HAC)`
`=>hat(HAC)=60^0`
Có `60^0=60^0`
`=>hat(B)=hat(HAC)`
refer
Cho tam giác ABC vuông tại A.vẽ AH vuông góc với BC tại H.Sao cho:\(BC^2=2AH^2+BH^{^{2^{ }}}+CH^2\) - Hoc24