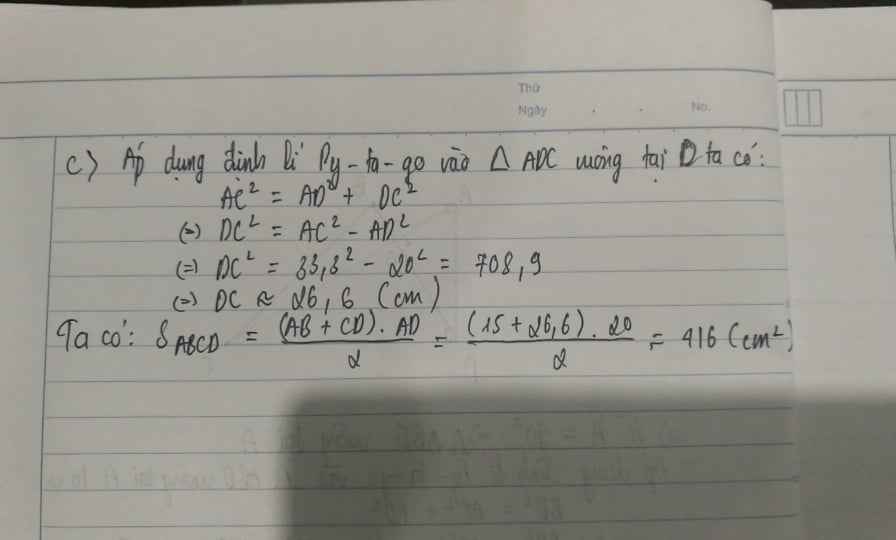cho hình thang ABCD vuông ( góc A,góc B =90 độ), AC vuông vs BD tại O.
a) tính OB, OD.
b) tính AC.
c) tính diện tích ABCD
Giúp với các bác ơi!!!!!!!!!!!!!!1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
M
13 tháng 9 2023
a) Ta có hình thang vuông ABCD, nên ta có: AB^2 + BC^2 = AC^2 AD^2 + DC^2 = AC^2
Vì AB = 15cm, AD = 20cm và ABCD là hình thang vuông, nên ta có: 15^2 + BC^2 = AC^2 20^2 + DC^2 = AC^2
Vì 2 đường chéo AC và BD vuông góc tại O, nên ta có: OB^2 + BC^2 = OC^2 OD^2 + DC^2 = OC^2
Vì ABCD là hình thang vuông, nên ta có: OB^2 + BC^2 = OD^2 + DC^2
Từ hai phương trình trên, ta có thể suy ra OB = OD.
b) Ta có thể tính đường chéo AC bằng cách sử dụng định lí Pythagoras trên tam giác vuông AOC: AC^2 = AO^2 + OC^2
Vì OB = OD, nên ta có AO = OD = OB.
Vậy, ta có: AC^2 = OB^2 + OC^2
c) Để tính diện tích SABCD, ta có thể sử dụng công thức
13 tháng 9 2023
a: ΔABD vuông tại A
=>BD^2=AB^2+AD^2=625
=>BD=25cm
ΔABD vuông tại A có AO là đường cao
nên BO*BD=BA^2 và DO*DB=DA^2 và AO^2=OD*OB
=>BO=15^2/25=9cm; DO=20^2/25=16cm; AO^2=9*16=144
=>AO=12cm
b: Xét ΔOAB vuông tại O và ΔOCD vuông tại O có
góc OAB=góc OCD
=>ΔOAB đồng dạng với ΔOCD
=>OA/OC=OB/OD
=>9/16=12/OC
=>OC=16*12/9=16*4/3=64/3cm
AC=12+64/3=100/3cm
c: \(S_{ABCD}=\dfrac{1}{2}\cdot AC\cdot BD=\dfrac{1}{2}\cdot\dfrac{100}{3}\cdot25=\dfrac{50}{3}\cdot25=\dfrac{1250}{3}\left(cm^2\right)\)
6 tháng 12 2018
ta có: góc D1 + D2 =90
mà D1 + C1 =90
=>D2=C1
xét tam giác ABD và DAC có
BAD=ADC
D2=C1(cmt)
=>ABD đồng dạng DAC (g-g)
=>AB/AD=AD/DC
<=>AD^2=AB.DC(1)
b) Bạn áp dung CT(1) tính AD sau đó tính DT abcd
c) Dựa vào hệ thức lượng trong tam giác vuông:
1/OA^2=1/ab^2 + 1/ad^2 =>OA=...
tính AC,BD bằng Pytago
OC= AC-OA
OD^2=OA*OC =>OD=....
OB=BD-OD
Chúc bạn học tốt !
CM
19 tháng 2 2018
a, Áp dụng các hệ thức lượng trong tam giác vuông ABD, tính được BD = 25cm, OB = 9cm, OD = 16cm
b, Áp dụng các hệ thức lượng trong tam giác vuông DAC tính được OA = 12cm, AC = 100 3 cm
c, Tính được S = 1250 3 c m 2
