B=1+1/3+1/6+1/10+....+1/630 = ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HT
8 tháng 8 2015
A = \(\frac{1}{1.3}+\frac{1}{3.5}+...+\frac{1}{99.101}\)
A = \(\frac{1}{2}\left(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+...+\frac{1}{99}-\frac{1}{101}\right)\)
A = \(\frac{1}{2}\left(1-\frac{1}{101}\right)=\frac{1}{2}.\frac{100}{101}\)
A = \(\frac{50}{101}\)
B = \(1+\frac{1}{3}+\frac{1}{6}+\frac{1}{10}+...+\frac{1}{630}\)
B = \(1+\frac{2}{6}+\frac{2}{12}+\frac{1}{20}+...+\frac{2}{1260}\)
B = \(1+2\left(\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+...+\frac{1}{35.36}\right)\)
B = \(1+2\left(\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+...+\frac{1}{35}-\frac{1}{36}\right)\)
B = \(1+2\left(\frac{1}{2}-\frac{1}{36}\right)=1+2.\frac{17}{36}\)
B = \(1+\frac{17}{18}\)
B = \(\frac{35}{18}\)
CB
2
U
9 tháng 8 2018
đặt \(A=1+\frac{1}{3}+\frac{1}{6}+\frac{1}{10}+...+\frac{1}{630}\)
\(A=\frac{2}{2}+\frac{2}{6}+\frac{2}{12}+\frac{2}{20}+...+\frac{2}{1260}\)
\(A=2\left(\frac{1}{1\cdot2}+\frac{1}{2\cdot3}+\frac{1}{3\cdot4}+\frac{1}{4\cdot5}+...+\frac{1}{35\cdot36}\right)\)
\(A=2\left(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{35}-\frac{1}{36}\right)\)
\(A=2\left(1-\frac{1}{36}\right)\)
\(A=2\cdot\frac{35}{36}\)
\(A=\frac{35}{18}\)
9 tháng 8 2018
ok Đặt A = 1/3 + 1/6 + 1/10 + ... + 1/630
Ta có : 1/2A = 2/6 + 2/12 + 2/20 + ... + 2/1260
1/2A = 2/2.3 + 2/3.4 + 2/4.5 + ... + 2/35.36
1/2A = 2 ( 1/2.3 + 1/3.4 + 1/4.5 + ... + 1/35.36 )
1/2A = 2 ( 1/2 - 1/3 + 1/3 - 1/4 + 1/4 - 1/5 + ... + 1/35 - 1/36 )
1/2A = 2 ( 1/2 - 1/36 )
1/2A= 2. 17/36
1/2A = 34/36
A = 34/36 : 1/2
A = 17/9
=> 1 + 17/9
= 26/9
ko chắc đúng
HT
9 tháng 8 2015
B = \(1+\frac{1}{3}+\frac{1}{6}+....+\frac{1}{630}=1+\frac{2}{6}+\frac{2}{12}+...+\frac{2}{1260}\)
B = \(1+2\left(\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{35.36}\right)\)
B = \(1+2\left(\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{35}-\frac{1}{36}\right)\)
B = \(1+2\left(\frac{1}{2}-\frac{1}{36}\right)=1+2.\frac{17}{36}\)
B = \(1+\frac{17}{18}\)
B = \(\frac{35}{18}\)
9 tháng 8 2015
\(A=\frac{1}{1x3}+\frac{1}{3x5}+\frac{1}{5x7}+...+\frac{1}{99x101}\)
\(A\)\(x2=\frac{2}{1x3}+\frac{2}{3x5}+\frac{2}{5x7}+...+\frac{2}{99x101}\)
\(A\)\(x2=1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{99}-\frac{1}{101}\)
\(A\)\(x2=1-\frac{1}{101}=\frac{100}{101}\)
\(A=\frac{100}{101}:2=\frac{100}{101}x\frac{1}{2}=\frac{50}{101}\)
IW
1
17 tháng 2 2019
a) 72.5–(2x+1)=630:972.5–(2x+1)=630:9
⇒245–2x–1=70⇒245–2x–1=70
⇒−2x=−22+70⇒−2x=−22+70
⇒−2x=−174⇒−2x=−174
⇒x=87⇒x=87
b)(10−4x)+120:23=17
10−4x+15=17
10−4x=17−15
10−4x=2
4x=10−2
4x=8
x=8:4
x=2
TS
4
HM
20 tháng 3 2020
a) 72,5 - (2x + 1) = 630 : 9
⇒ 72,5 - (2x + 1) = 70
⇒ 2x + 1 = 2,5
⇒ 2x = 1,5
⇒ x = 0,75
HM
20 tháng 3 2020
b) (10 - 4x) + 120 : 23 = 17
⇒ (10 - 4x) + 120 : 8 = 17
⇒ (10 - 4x) + 15 = 17
⇒ 10 - 4x = 2
⇒ 4x = 8
⇒ x = 2
Vậy x = 2
PT
1
TL
1
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
11 tháng 9 2023
\(a,0,\left(123\right)+0,\left(876\right)=\dfrac{123}{999}+\dfrac{876}{999}=\dfrac{999}{999}=1\left(đpcm\right)\\ b,0,\left(123\right).3+0,\left(630\right)=\dfrac{123}{999}.3+\dfrac{630}{999}=\dfrac{369}{999}+\dfrac{630}{999}=\dfrac{999}{999}=1\left(đpcm\right)\)
MT
3
5 tháng 3 2020
72 x 5-(2x+1)=630:9
<=> 49 x 5-2x-1=70
<=> 245-2x-1=70
<=> -2x+244=70
<=> -2x=-174
<=> x=87
5 tháng 3 2020
tìm x biết:
a, 72.5-(2x+1)=630:9
49.5-(2x+1)=70
245-(2x+1)=70
2x+1=245-70
2x+1=175
2x=175-1
2x=174
x=174:2
x=87
Vậy x=87
b, (10-4x)+120:23=17
(10-4x)+120:8=17
(10-4x)+15=17
10-4x=17-15
10-4x=2
4x=10-2
4x=8
x=8:4
x=2
Vậy x=2
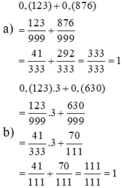
B = \(1+\frac{1}{3}+\frac{1}{6}+\frac{1}{10}+...+\frac{1}{630}\)
B = \(1+\frac{2}{6}+\frac{2}{12}+\frac{2}{20}+...+\frac{2}{1260}\)
B = \(1+2.\left(\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+...+\frac{1}{35.36}\right)\)
B = \(1+2.\left(\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+..+\frac{1}{35}-\frac{1}{36}\right)\)
B = \(1+2.\left(\frac{1}{2}-\frac{1}{36}\right)=1+2.\frac{17}{36}=1+\frac{17}{18}\)
B = \(\frac{35}{18}\)
(x+1) + (x+4) + (x+7) + ....+ (x+28) = 155