ΔABC đều cạnh 2a AH là đường cao
1. \(\overrightarrow{AB}\).\(\overrightarrow{AC}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

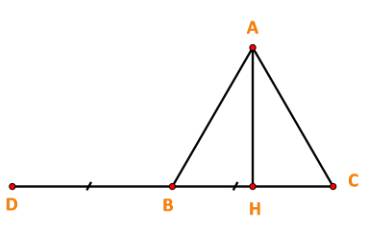
a) Vẽ vecto \(\overrightarrow {BD} = \overrightarrow {CB} \). Ta có:
\((\overrightarrow {CB} ,\overrightarrow {BA} ) = (\overrightarrow {BD} ,\overrightarrow {BA} ) = \widehat {DBA} = {120^o}\)
Vậy \(\overrightarrow {CB} .\overrightarrow {BA} = \left| {\overrightarrow {CB} } \right|.\left| {\overrightarrow {BA} } \right|\cos (\overrightarrow {CB} ,\overrightarrow {BA} ) = a.a.\cos {120^o} = {a^2}.\left( { - \frac{1}{2}} \right) = - \frac{{{a^2}}}{2}.\)
b) Vì \(AH \bot BC\) nên \[(\overrightarrow {AH} ,\overrightarrow {BC} ) = {90^o}\], suy ra \(\cos (\overrightarrow {AH} ,\overrightarrow {BC} ) = \cos {90^o} = 0.\)
Vậy \(\overrightarrow {AH} .\overrightarrow {BC} = \left| {\overrightarrow {AH} } \right|.\left| {\overrightarrow {BC} } \right|.\cos (\overrightarrow {AH} ,\overrightarrow {BC} ) = 0.\)

Có vẻ không đúng.
Giả sử \(\overrightarrow{AB}+\overrightarrow{MB}+\overrightarrow{MA}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MB}+\left(\overrightarrow{MA}+\overrightarrow{AB}\right)=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MB}+\overrightarrow{MB}=\overrightarrow{0}\)
\(\Leftrightarrow2\overrightarrow{MB}=\overrightarrow{0}\)
\(\Leftrightarrow M\equiv B\) (Vô lí)

+) \(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \widehat {ABC} = 60^\circ \)
+) Dựng hình bình hành ABCD, ta có: \(\overrightarrow {AD} = \overrightarrow {BC} \)
\( \Rightarrow \left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {AB} ,\overrightarrow {AD} } \right) = \widehat {BAD} = 120^\circ \)

+), Ta có: ABC là tam giác đều, H là trung điểm BC nên \(AH \bot BC\)
\(\left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {AH} ,\overrightarrow {AD} } \right) = \widehat {HAD} = 90^\circ \)
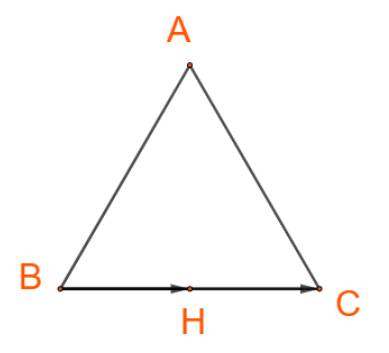
+) Hai vectơ \(\overrightarrow {BH} \) và \(\overrightarrow {BC} \)cùng hướng nên \(\left( {\overrightarrow {BH} ,\overrightarrow {BC} } \right) = 0^\circ \)
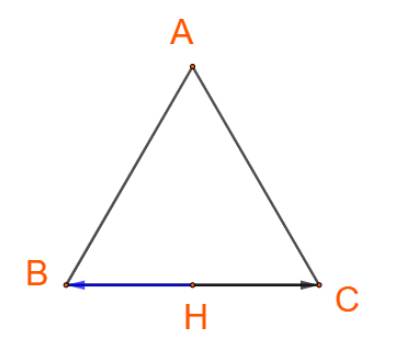
+) Hai vectơ \(\overrightarrow {HB} \) và \(\overrightarrow {BC} \)ngược hướng nên \(\left( {\overrightarrow {HB} ,\overrightarrow {BC} } \right) = 180^\circ \)

H đối xứng B qua G \(\Rightarrow\overrightarrow{BH}=2\overrightarrow{BG}=2\left(\dfrac{1}{3}\overrightarrow{BA}+\dfrac{1}{3}\overrightarrow{BC}\right)=-\dfrac{2}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{BC}\)
\(\overrightarrow{AH}=\overrightarrow{AB}+\overrightarrow{BH}=\overrightarrow{AB}-\dfrac{2}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{BC}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)\)
\(=\dfrac{1}{3}\overrightarrow{AB}-\dfrac{2}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}=\dfrac{2}{3}\overrightarrow{AC}-\dfrac{1}{3}\overrightarrow{AB}\)
\(\overrightarrow{CH}=\overrightarrow{CA}+\overrightarrow{AH}=-\overrightarrow{AC}+\dfrac{2}{3}\overrightarrow{AC}-\dfrac{1}{3}\overrightarrow{AB}=-\dfrac{1}{3}\overrightarrow{AB}-\dfrac{1}{3}\overrightarrow{AC}\)
\(\overrightarrow{MH}=\overrightarrow{MA}+\overrightarrow{AH}=-\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AC}+\dfrac{2}{3}\overrightarrow{AC}-\dfrac{1}{3}\overrightarrow{AB}\)
\(=-\dfrac{5}{6}\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AC}\)

Ta có: \(AH \bot CB \Rightarrow (\overrightarrow {AH} ,\overrightarrow {CB} ) = {90^o} \Leftrightarrow \cos (\overrightarrow {AH} ,\overrightarrow {CB} ) = 0 \Leftrightarrow \overrightarrow {AH} .\overrightarrow {CB} = 0\)
a) \(\overrightarrow {AB} .\overrightarrow {AH} - \overrightarrow {AC} .\overrightarrow {AH} = (\overrightarrow {AB} - \overrightarrow {AC} ).\overrightarrow {AH} = \overrightarrow {CB} .\overrightarrow {AH} = 0\)
\( \Leftrightarrow \overrightarrow {AB} .\overrightarrow {AH} = \overrightarrow {AC} .\overrightarrow {AH} \)
b) \(\overrightarrow {AB} .\overrightarrow {BC} - \overrightarrow {HB} .\overrightarrow {BC} = (\overrightarrow {AB} - \overrightarrow {HB} ).\overrightarrow {BC} = (\overrightarrow {AB} + \overrightarrow {BH} ).\overrightarrow {BC} = \overrightarrow {AH} .\overrightarrow {BC} = 0\)
\( \Leftrightarrow \overrightarrow {AB} .\overrightarrow {BC} = \overrightarrow {HB} .\overrightarrow {BC} \)

M, N là trung điểm AB và AC nên MN là đường trung bình tam giác ABC
\(\Rightarrow MN||BC\Rightarrow\overrightarrow{MN}\) và \(\overrightarrow{BC}\) cùng phương
\(\overrightarrow{AB}.\overrightarrow{AC}=AB.AC.cosA=2a.2a.cos60^0=2a^2\)
\(2\overrightarrow{AB}.3\overrightarrow{HC}=6\left(\overrightarrow{AH}+\overrightarrow{HB}\right).\overrightarrow{HC}=6\overrightarrow{AH}.\overrightarrow{HC}+6\overrightarrow{HB}.\overrightarrow{HC}\)
\(=6\overrightarrow{HB}.\overrightarrow{HC}=-6HC^2=-6a^2\)