Bài 1.Tìm số phức z thoả mãn 
giúp mik vs
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left(1+2i\right)z-5=3i\Leftrightarrow\left(1+2i\right)z=5+3i\)
\(\Rightarrow z=\dfrac{5+3i}{1+2i}=\dfrac{11}{5}-\dfrac{7}{5}i\)
\(\Rightarrow\overline{z}=\dfrac{11}{5}+\dfrac{7}{5}i\)
2.
Đề câu này là: \(3z-5\overline{z}-6+10i=0\) đúng không nhỉ?

Vì \(\hept{\begin{cases}\left(x+1\right)^2\ge0\\y^{2018}\ge0\end{cases}}\) => \(\left(x+1\right)^2+y^{2018}=0\)
<=> \(\hept{\begin{cases}\left(x+1\right)^2=0\\y^{2018}=0\end{cases}}\)<=> \(\hept{\begin{cases}x=-1\\y=0\end{cases}}\)

Chọn D.
Ta có P = |2z + 1 = 2i| nên 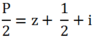
Ta cần tìm giá trị lớn nhất, giá trị nhỏ nhất của: 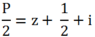
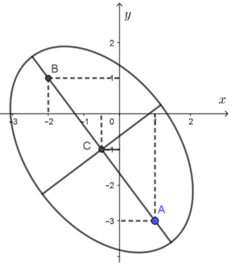
Ta có z1 = 1 - 3i; z2 = -2 + i và z0 = -1/2 - i
Ta thấy: ![]()
Tính 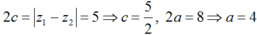
Suy ra 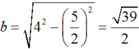
Vậy Max P = 2.4 = 8 và 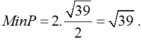
Đặt \(z=a+bi,\left(a,b\inℝ\right)\).
Ta có: \(\left(1+2i\right)z+5\overline{z}=4-2i\)
\(\Leftrightarrow\left(1+2i\right)\left(a+bi\right)+5\left(a-bi\right)=4-2i\)
\(\Leftrightarrow a-2b+\left(2a+b\right)i+5a-5bi-4+2i=0\)
\(\Leftrightarrow\left(a-2b+5a-4\right)+\left(2a+b-5b+2\right)i=0\)
\(\Leftrightarrow\hept{\begin{cases}6a-2b=4\\2a-4b=-2\end{cases}}\Leftrightarrow a=b=1\).
Vậy \(z=1+i\).