Bài 4 - Mã đề 112 đề thi môn Toán năm 2017
Tìm tham số m là số thực để có đường thằng d:
y = (2m - 1)x + 3 + m vuông vóc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = x³- 3x² + 1
A. m = 3/2 B. m = 3/4
C. m = -1/2 D. m = 1/4
cứu vs .mik tích


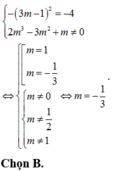

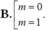
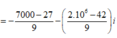
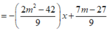

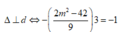
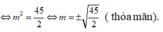
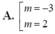

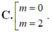
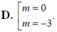
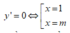
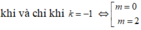
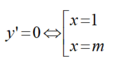
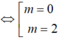
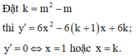
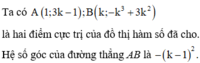

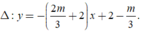
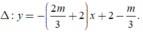 có một VTCP là
có một VTCP là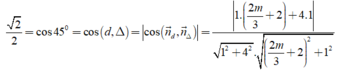
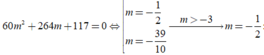 thỏa mãn
thỏa mãn
Bài giải:
Để có thể giải quyết được bài toán trên, bạn đọc cần tìm được 2 điểm cực trị của hàm số và viết phương trình đường thẳng đi qua chúng.
Hàm số y = x³ - 3x² + 1 có y’ = 3x² - 6x = 0 ⇔ x= 0 hoặc x = 2
x = 0 ⇒ y = 1
x = 2 ⇒ y = -3
⇒ Hàm số có hai điểm cực trị A (0;1), B (2; -3). Đường thẳng đi qua hai điểm cực trị của hàm số có phương trình 2x + y – 1 = 0.
Đường thẳng (2m - 1)x - y + 3 + m = 0 vuông góc với đường thẳng
2x + y – 1 = 0 ⇔ hai véc-tơ pháp tuyến vuông góc với nhau.
a1. a2 + b1.b2 = 0 ⇔ (2m - 1) 2 + (-1)1 = 0 ⇔ 4m - 2 - 1 = 0 ⇔ m = 3/4.
Đáp án đúng là B.
tích cho mik nha.