với những giá trị nào của a thì:
a) a2>a
b) a2<a
c) a2=a
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 6 2023
2:
a: =>a^2+2ab+b^2-2a^2-2b^2<=0
=>-(a^2-2ab+b^2)<=0
=>(a-b)^2>=0(luôn đúng)
b; =>a^2+b^2+c^2+2ab+2ac+2bc-3a^2-3b^2-3c^2<=0
=>-(2a^2+2b^2+2c^2-2ab-2ac-2bc)<=0
=>(a-b)^2+(b-c)^2+(a-c)^2>=0(luôn đúng)
CM
24 tháng 12 2019
Ta có: x + y = a 2 + a + 1 x - y = - a 2 + a - 1 ⇔ x + y = a 2 + a + 1 2 x = 2 a ⇔ y = a 2 + 1 x = a
Do đó 3 x + y = a 2 + 3 a + 1 = a + 3 2 2 - 5 4 ≥ - 5 4 . Dấu bằng xảy ra khi a = - 3 2 .
17 tháng 9 2021
\(M=a^2+ab+b^2-3a-3b+2001\)
\(\Rightarrow2M=2a^2+2ab+2b^2-6a-6b+4002\)
\(=\left[\left(a+b\right)^2-2\left(a+b\right).2+4\right]+\left(a^2-2a+1\right)+\left(b^2-2b+1\right)+3996\)
\(=\left(a+b-2\right)^2+\left(a-1\right)^2+\left(b-1\right)^2+3996\ge3996\)
\(\Rightarrow M\ge1998\)
\(minM=1998\Leftrightarrow a=b=1\)
LT
0
CM
2 tháng 7 2019
Điều kiện x ≠ 2 và x ≠ 0
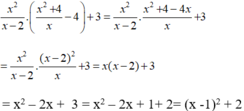
Vì x - 1 2 ≥ 0 nên x - 1 2 + 2 ≥ 2 với mọi giá trị của x.
Khi đó giá trị nhỏ nhất của biểu thức bằng 2 khi x = 1.
Vậy biểu thức đã cho có giá trị nhỏ nhất bằng 2 tại x = 1.
CM
16 tháng 1 2017
Điều kiện x ≠ -2 và x ≠ 0
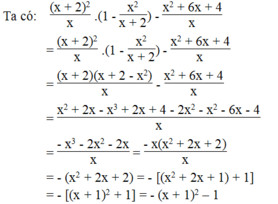
Vì x + 1 2 ≥ 0 nên - x + 1 2 ≤ 0 ⇒ - x + 1 2 - 1 ≤ - 1
Khi đó biểu thức có giá trị lớn nhất bằng -1 khi x = -1
Vậy biểu thức đã cho có giá trị lớn nhất bằng -1 tại x = -1.
LP
1
a. mọi a thuộc Z
b. ko có a
c. a \(\in\left\{-1;0;1\right\}\)