Giúp mình giải tìm giá trin lớn nhất và nhỏ nhất của hàm số y=cos pi x trên đoạn [1/4;3/2]
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PN
1
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 7 2021
\(-1\le cos\left(\sqrt{x}+\dfrac{\pi}{4}\right)\le1\Rightarrow-5\le y\le5\)
\(y_{max}=5\) khi \(cos\left(\sqrt{x}+\dfrac{\pi}{4}\right)=1\)
\(y_{min}=-5\) khi \(cos\left(\sqrt{x}+\dfrac{\pi}{4}\right)=-1\)
PN
1
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 7 2021
Đề là:
\(y=\sqrt{4-3cos^23x}+1\) đúng không nhỉ?
Ta có:
\(0\le cos^23x\le1\Rightarrow1\le\sqrt{4-3cos^23x}\le2\)
\(\Rightarrow2\le y\le3\)
\(y_{min}=2\) khi \(cos^23x=1\)
\(y_{max}=3\) khi \(cos3x=0\)
PN
1
HP
1 tháng 7 2021
\(y=-1-cos^2\left(2x+\dfrac{\pi}{3}\right)\)
\(=-\dfrac{3}{2}+\dfrac{1}{2}-cos^2\left(2x+\dfrac{\pi}{3}\right)\)
\(=-\dfrac{3}{2}-\dfrac{1}{2}\left[2cos^2\left(2x+\dfrac{\pi}{3}\right)-1\right]\)
\(=-\dfrac{3}{2}-\dfrac{1}{2}cos\left(4x+\dfrac{2\pi}{3}\right)\)
Vì \(cos\left(4x+\dfrac{2\pi}{3}\right)\in\left[-1;1\right]\)
\(\Rightarrow min=-\dfrac{3}{2}-\dfrac{1}{2}=-2\Leftrightarrow cos\left(4x+\dfrac{2\pi}{3}\right)=1\)
\(\Rightarrow max=-\dfrac{3}{2}+\dfrac{1}{2}=-1\Leftrightarrow cos\left(4x+\dfrac{2\pi}{3}\right)=-1\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 10 2021
\(f'\left(x\right)=2-\dfrac{\pi}{2}sin\left(\dfrac{\pi x}{3}\right)=\dfrac{1}{2}\left(4-\pi sin\left(\dfrac{\pi x}{2}\right)\right)\)
Do \(\left|\pi sin\left(\dfrac{\pi x}{2}\right)\right|\le\pi< 4\Rightarrow f'\left(x\right)>0\) ; \(\forall x\)
\(\Rightarrow f\left(x\right)\) đồng biến trên R
\(\Rightarrow f\left(x\right)_{min}+f\left(x\right)_{max}=f\left(-2\right)+f\left(2\right)=-4+cos\left(-\pi\right)+4+cos\left(\pi\right)=-2\)
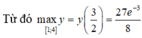
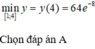
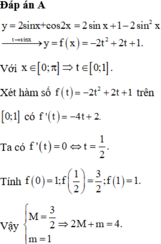
\(x\in\left[\dfrac{1}{4};\dfrac{3}{2}\right]\Rightarrow\pi x\in\left[\dfrac{\pi}{4};\dfrac{3\pi}{2}\right]\)
\(\Rightarrow cos\left(\pi x\right)\in\left[-1;\dfrac{\sqrt{2}}{2}\right]\)
\(y_{max}=\dfrac{\sqrt{2}}{2}\) khi \(x=\dfrac{1}{4}\)
\(y_{min}=-1\) khi \(x=1\)