Ai giup voi a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1+1=2, câu quá dễ, ko phải ko biết làm mà là cố ý

- Cây cỏ là thức ăn của con nai, con nai là thức ăn của con hổ.
- Cây rau muống là thức ăn của con lợn, con lợn là thức ăn của con người.
cây cỏ là thức ăn của con dê là thức ăn của con hổ
cây cà rốt là thức ăn của con thỏ là thức ăn của con người
ko viết mũi tên nên hơi khó hiểu nha
tick nếu đúng

4 has not been - broke
5 did you - was
6 have youy ever been
II
1 go
2 were
3 eats
7 does - won't worry
8 had played - would have won
9 will - do
10 were - would go
14 would have written
15 won't go
16 tries
17 spoke
19 finish - will go
20 see - ask
Rewrite
1 The man who doesn't work hard can't earn more money
3 If my friend and I had enough money, we would buy a house of our town
4 If the weather were better now, we could go for a walk
5 If I knew his addres, I would give it to you
6 If he worked slowly enough, he wouldn't make
7 If I were sent to proson, she would visit me
8 If I won a big prize in a lottery, I would give up my job
9 If the doctor weren't so late, he could see many patients
10 If tickets weren't expensive, we would visit them in Ha Noi
III
1 were
2 would visit
3 would give


chữ số hàng nghìn có thể lập từ 3 chữ số trên ( 2;5;8)
chữ số hàng trăm có thể lập được từ 4 chữ số trên (0;2;5;8)
chữ số hàng chục có thể lập được từ 4 chữ số trên (0;2;5;8)
chữ số hàng đơn vị có thể lập được từ 1 chữ số trên ( 0 chia hết cho cả 2 lẫn 5)
vậy ta có : 3 x 4 x 4 x 1 = 48 số
vậy có tất cả 48 số có 4 chữ số phù hợp với điều kiện của đề bài

\(\left(a-1\right)\left(b-1\right)\left(c-1\right)=\left(ab-a-b+1\right)\left(c-1\right)=abc-ac-bc+c-ab+a+b-1=abc+\left(a+b+c\right)-\left(ab+bc+ca\right)-1\)\(\left(a-\dfrac{1}{b}\right)\left(b-\dfrac{1}{c}\right)\left(c-\dfrac{1}{a}\right)\ge\left(a-\dfrac{1}{a}\right)\left(b-\dfrac{1}{b}\right)\left(c-\dfrac{1}{c}\right)\)
\(\Leftrightarrow\dfrac{\left(ab-1\right)\left(bc-1\right)\left(ca-1\right)}{abc}\ge\dfrac{\left(a^2-1\right)\left(b^2-1\right)\left(c^2-1\right)}{abc}\)
\(\Leftrightarrow\left(ab-1\right)\left(bc-1\right)\left(ca-1\right)\ge\left(a^2-1\right)\left(b^2-1\right)\left(c^2-1\right)\) (do a,b,c>1)
\(\Leftrightarrow a^2b^2c^2+\left(ab+bc+ca\right)-\left(ab^2c+a^2bc+abc^2\right)-1=a^2b^2c^2+\left(a^2+b^2+c^2\right)-\left(a^2b^2+b^2c^2+c^2a^2\right)\)
\(\Leftrightarrow ab+bc+ca-a^2bc-ab^2c-abc^2=a^2+b^2+c^2-a^2b^2-b^2c^2-c^2a^2\)
\(\Leftrightarrow ab+bc+ca-a^2bc-ab^2c-abc^2-a^2-b^2-c^2+a^2b^2+b^2c^2+c^2a^2=0\)
\(\Leftrightarrow bc\left(a^2-1\right)+ca\left(b^2-1\right)+ab\left(c^2-1\right)+a^2\left(b^2-1\right)+b^2\left(c^2-1\right)+c^2\left(a^2-1\right)=0\)
(luôn đúng do a,b,c>1)

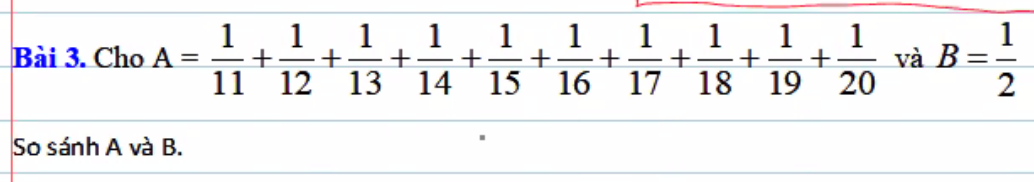 ai giup em voi a
ai giup em voi a giup mk voi a , mk dang can gap
giup mk voi a , mk dang can gap  ai giup minh voi a minh can gap lam TvT
ai giup minh voi a minh can gap lam TvT 

TC2: a) Ta có : \(cos^2\alpha=1-sin^2\alpha=1-\left(\frac{2}{3}\right)^2=\frac{5}{9}\)
\(\Rightarrow cos\alpha=\sqrt{\frac{5}{9}}=\frac{\sqrt{5}}{3}\)
\(\Rightarrow\hept{\begin{cases}tan\alpha=\frac{sin\alpha}{cos\alpha}=\frac{\frac{2}{3}}{\frac{\sqrt{5}}{3}}=\frac{2}{\sqrt{5}}\\cot\alpha=\frac{cos\alpha}{sin\alpha}=\frac{\frac{\sqrt{5}}{3}}{\frac{2}{3}}=\frac{\sqrt{5}}{2}\end{cases}}\)
b)Ta có :\(A=\frac{sin\alpha-cos\alpha}{sin\alpha+cos\alpha}=\frac{\frac{2}{3}-\frac{\sqrt{5}}{3}}{\frac{2}{3}+\frac{\sqrt{5}}{3}}=\frac{2-\sqrt{5}}{2+\sqrt{5}}=\frac{\left(2-\sqrt{5}\right)^2}{4-5}=4\sqrt{5}-9\)