Cho tam giác ABC vuông tại A có BC = 5 cm, đường cao AH = 12/5 cm. Tính BH, CH.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BN
2
5 tháng 7 2021
Áp dụng đ/lí pytago vào tam giác ABC vuông tại A CÓ:
AB^2+AB^2=BC^2
Hay: 12^2+5^2=169=BC^2 => BC=13cm
ÁP dụng hệ thức ta có: +) AB^2=BH.BC
Hay: BH=AB^2:BC=144:13 =144/13(cm)
Ta có CH=BC-BH=13-144/13=25/13(cm)
DO KHÔNG RÕ CÂU HỎI NÊN MÌNH CŨNG KO CHẮC LẮM...
HỌC TỐT!!!
26 tháng 9 2021
Bài 5:
Ta có: \(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH\left(BH+9\right)=400\)
\(\Leftrightarrow BH^2+25HB-16HB-400=0\)
\(\Leftrightarrow BH=16\left(cm\right)\)
hay BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AC=15\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)
TH
Cho tam giác ABC vuông tại A có đường cao AH biết AB = 6 cm BC = 12 cm Tính độ dài đoạn thẳng BH, CH
1
AH
Akai Haruma
Giáo viên
20 tháng 12 2023
Lời giải:
Áp dụng công thức hệ thức lượng trong tam giác vuông ta có:
$AB^2=BH.BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{6^2}{12}=3$ (cm)
$CH=BC-BH=12-3=9$ (cm)
7 tháng 9 2016
Đặt BH = x (0 < x < 25) (cm) => CH = 25 - x (cm)
Ta có : \(AH^2=BH.CH\Rightarrow x\left(25-x\right)=144\Leftrightarrow x^2-25x+144=0\)
\(\left(x-9\right)\left(x-16\right)=0\) \(\Leftrightarrow\left[\begin{array}{nghiempt}x=9\\x=16\end{array}\right.\) (tm)
Nếu BH = 9 cm thì CH = 16 cm\(\Rightarrow AB=\sqrt{AH^2+BH^2}=\sqrt{9^2+12^2}=15\left(cm\right)\)
\(AC=\sqrt{AH^2+CH^2}=\sqrt{12^2+16^2}=20\left(cm\right)\)
Nếu BH = 16 cm thì CH = 9 cm
\(\Rightarrow AB=\sqrt{AH^2+BH^2}=\sqrt{12^2+16^2}=20\left(cm\right)\)
\(AC=\sqrt{AH^2+CH^2}=\sqrt{9^2+12^2}=15\left(cm\right)\)
9 tháng 9 2016
Gỉa sử \(\Delta ABC\) có AB>AC
\(AB.AC=AH.BC=12.25=300\)
\(\Leftrightarrow2AB.AC=2.300=600\)
Áp dụng định lý Pytago cho \(\Delta ABC\) vuông tại A ta có:
\(AB^2+AC^2=BC^2=25^2=625\) (1)
\(\left(1\right)\Rightarrow AB^2+AC^2-2AB.AC=625-600\)
\(\Leftrightarrow\left(AB-AC\right)^2=25\Leftrightarrow AB-AC=5\) (a) (Vì AB>AC \(\Rightarrow AB-AC>0\))
\(\left(1\right)\Rightarrow AB^2+AC^2+2AB.AC=600+625=1225\)
\(\Leftrightarrow\left(AB+AC\right)^2=1225\Rightarrow AB+AC=35\) (b)
Cộng vế vs vế của (a) và (b) ta được: \(2AB=40\Rightarrow AB=20\)
\(\Rightarrow AC=AB-5=20-5=15\)
Xét \(\Delta ABC\) vuông tại A, \(AH\perp BC\)\(\Rightarrow\) theo hệ thức lượng trong tam giác vuông ta có:
\(AB^2=BH.BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{20^2}{25}=16\)
\(\Rightarrow CH=BC-BH=25-16=9\)
23 tháng 7 2021
Bài 1:
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=15^2-9^2=144\)
hay AC=12(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{9^2}{15}=\dfrac{81}{15}=5.4\left(cm\right)\\CH=\dfrac{12^2}{15}=\dfrac{144}{15}=9,6\left(cm\right)\end{matrix}\right.\)
Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:
\(AH^2+HB^2=AB^2\)
\(\Leftrightarrow AH^2=9^2-5.4^2=51,84\)
hay AH=7,2(cm)
17 tháng 5 2022
1: \(BC=\sqrt{12^2+9^2}=15\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=7,2\left(cm\right)\)
\(BH=\dfrac{AB^2}{BC}=\dfrac{144}{15}=9,6\left(cm\right)\)
CH=5,4(cm)
2: \(BC=\sqrt{2+2}=2\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=1\left(cm\right)\)
\(BH=CH=AH=1\left(cm\right)\)
N
2
12 tháng 9 2021
Ta có: BC=BH+CH
nên BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=15\left(cm\right)\\AC=20\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)
T
cho tam giác vuông ABC vuông tại A sao cho đường cao AH biết AB= 3 cm , AC = 4 cm , tính BC AH BH CH
2
S
13 tháng 9 2023
Áp dụng định lý Pytago vào tam giác ABC(góc A=90) có:
BC2=AB2+AC2
<=>BC2=32+42
<=>BC2=25
<=>BC=5(cm)
Áp dụng HTL vào tam giác ABC vuông tại A có đường cao AH được:
AB.AC=BC.AH
<=>3.4=5.AH
<=> AH=\(\dfrac{3.4}{5}\)
<=>AH=2,4(cm)
Áp dụng định lý Pytago vào tam giác AHB vuông tại H có:
AB2=AH2+BH2
<=>BH2=32-2,42
<=>BH2=3,24
<=>BH=1,8(cm)
Ta có:BC=BH+CH
=>CH=BC-BH=5-1,8=3,2(cm)
Vậy BC=5cm;AH=2,4cm;BH=1,8cm;CH=3,2cm
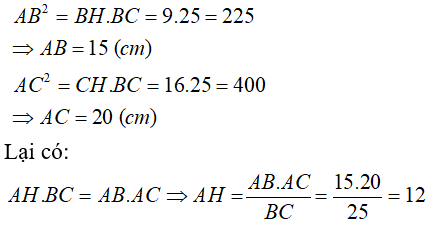
Ta có \(\Delta HBA\approx\Delta HAC\Rightarrow\frac{HB}{HA}=\frac{HA}{HC}\)
=> HB.HC = HA2
=> 2HB.HC = \(\frac{288}{25}\)
mà HB + HC = BC = 5 (1)
=> HB2 + HC2 + 2HB.HC = 25
<=> HB2 + HC2 - 2.HB.HC = 1,96
<=> HB - HC = 1,4 (2)
Từ (1) và (2) => HB = 3,2 ; HC = 1,8
Mình hỏi tý nè :
Sao cái tam giác ABC vuông tại A rồi thì AB là chiều cao chứ ạ. Hì hì mình nói có gì sai mọi người bảo mình nha.