Cho một số có hai chữ số có dạng ab .Chứng tỏ rằng ab+ba chia hết a+b
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
XO
14 tháng 8 2019
a) Ta có : ab - ba = (a0 + b) - (b0 + a)
= (10 x a + b) - (10 x b + a)
= (10 x a - a) - (10 x b - b)
= 9 x a - 9 x b
= 9 x (a - b) \(⋮\)9
=> (ab - ba) \(⋮\)9 (đpcm)
b) Ta có : ab + ba = a0 + b + b0 + a
= 10 x a + b + b x 10 + a
= (10 x a + a) + (10 x b + b)
= 11 x a + 11 x b
= 11 x (a + b) \(⋮\)11
=> (ab + ba) \(⋮\)11 (đpcm)
9 tháng 10 2014
Ta có ab + ba
= 10a + b +10b + a
= 10(a+b) + (a+b) chia hết cho (a+b)
LV
18 tháng 8 2018
Ta có : \(ab+ba\)
\(=10a+b+10b+a\)
\(=10\left(a+b\right)+\left(a+b\right)⋮\left(a+b\right)\)
\(\Leftrightarrow ab+ba⋮\left(a+b\right)\)
Vậy..........
10 tháng 4 2018
c, Ta có ab+ba = 10a + 10b + a + b=11a + 11b
Vậy ab+ba chia hết cho 11
14 tháng 1 2016
a) ab + ba
= 10a + b + 10b + a
= 11a + 11b = 11(a+b)
Chia hết cho a + b
15 tháng 1 2016
a) ab + ba
= 10a + b + 10b + a
= 11a + 11b = 11(a+b)
Chia hết cho a + b
27 tháng 7 2018
b. Ta có :
ab+ba =a0+b +b0 + a=(a0 + a) + (b0 + b) = aa + bb chia hết cho 11
3 tháng 6 2018
a) Ta có : ab - ba
= ( 10 x a + b ) - ( 10 x b + a )
= ( 10 x a - a ) - ( 10 x b - b )
= 9 x a - 9 x b
= 9 x ( a - b )
\(\Rightarrow\)ab - ba chia hết cho 9
b) Ta có: ab + ba
= ( 10 x a + b ) + ( 10 x b + a )
= ( 10 x a + a ) + ( 10 x b + b )
= 11 x a + 11 x b
= 11 x ( a + b )
\(\Rightarrow\)ab + ba chia hết cho 11
Nhớ k chị nha. Chúc em học tốt.
17 tháng 7 2019
a)Ta có:
ab-ba =a.10+b-b.10-a
=a.9-b.9
Mà a > b nên thương nhỏ nhất của hai số sẽ bằng 9.
=> ab-ba luôn chia hết cho 9
b) ab+ba =a.10+b+b.10+a
=a.11+b.11
=(a+b).11
=> ab+ba luôn chia hết cho 11
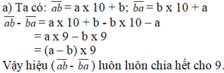
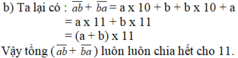
Ta co:
ab + ba = (10 . a+ b) + (10 .a + b)
= (11 . a) + (11 . b)
= 11. (a + b) chia het cho ab
Vay ab + ba chia het cho a+ b