cho tập hợp : A =( a1;a2;a3;...;a15) trong đó mỗi số trong tập hợp A đều khác nhau và là số nguyên dương không vượt quá 28; B= ( b1;b2;b3; .......; b14 ) trong đó mỗi số trong tập hợp B đều khác nhau và là số nguyên dương không vượt quá 28. chứng tỏ rằng trong hai tập hợp ít nhất có 1 cặp bằng nhau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án D
Số phần tử của tập ![]()
Để ![]() chia hết cho 5 điều kiện cần và đủ là
chia hết cho 5 điều kiện cần và đủ là ![]() hay
hay ![]()
Nếu ![]() thì lấy trong 7 chữ số 1,2,...,7
thì lấy trong 7 chữ số 1,2,...,7
Vậy có ![]() số tận cùng bằng 0
số tận cùng bằng 0
Nếu ![]() thì các số
thì các số ![]() là
là ![]() số
số
Vây xác suất để số đó chia hết cho 5 là 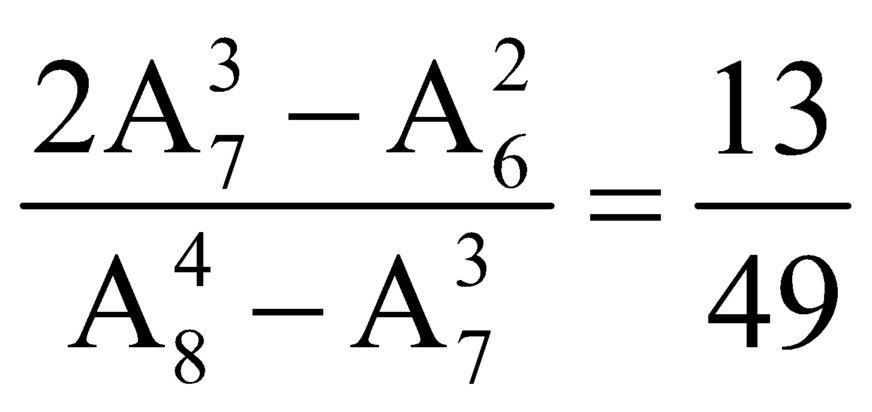

a)
7 ∈ A 1 ∉ A e ∈ A A ⊂ B 3 , 7 ⊂ A 1 , 3 , e ⊂ B
b) Tập hợp B gồm có 4 phần tử.

a1: A = {57;357;3651}
a2: B = {57;85} ; C = {57;357} ; D = {57;814} ; E = {57;3651} ; G = {85;357} ; H = {85;814} ; L = {85;3651} ; K = {357;814} ; O = {357;3651}
M = {814;3651}
b/ B = {15;20;25;30;35;40;45;50;55;60;65;70;75;80;85;90;95}
Có: (95 - 15) : 5 + 1 = 17 (phần tử)

Nối A 1 ∈ E với m điểm B 1 , B 2 , B 3 , . .. , B m ∈ F ta có m đoạn thẳng A 1 B 1 , A 1 B 2 , A 1 B 3 , . .. , A 1 B m . Lần lượt nối A 1 , A 2 , A 3 , . .. , A n ∈ E với m điểm B 1 , B 2 , B 3 , . .. , B m ∈ F ta có số đoạn thẳng có một đầu thuộc E và một đầu thuộc F là m.n đoạn thẳng.

Đáp án C.
Ta có y ' = 3 x 2 - 12 x + 9 .
Gọi M x 0 ; y 0 là tiếp điểm của tiếp tuyến đi qua A của đồ thị hàm số.
Lúc này tiếp tuyến có phương trình
y = 3 x o 2 - 12 x 0 + 9 x - x 0 + x 0 3 - 6 x 0 2 + 9 x 0 - 1
Tiếp tuyến đi qua A 1 ; m ⇒ m = 3 x 0 2 - 12 x 0 + 9 1 - x 0 + x 0 3 - 6 x 0 2 + 9 x 0 - 1
⇔ m = - 2 x 0 3 + 9 x 0 2 - 12 x 0 + 8 (*).
Để có đúng một tiếp tuyến của đồ thị hàm số đi qua A thì phương trình (*) có duy nhất một nghiệm.
Xét hàm số f ( x ) = - 2 x 0 3 + 9 x 0 2 - 12 x 0 + 8 có bảng biến thiên
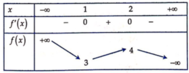
Để phương trình (*) có nghiệm duy nhất thì m > 4 m < 3 ⇔ m ∈ - ∞ ; 3 ∪ 4 ; + ∞ .
Vậy ta chọn C.




Giả sử: các phần tử trong tập hợp A khác tất cả các phần tử trong tập hợp B
Mà A có 15 phần tử là các số nguyên dương không vượt quá 28
B có 14 phần tử là các số nguyên dương không vượt quá 28
=> có 15 + 14 = 29 phần tử khác nhau không và không vượt quá số 28. Điều này không đúng vì Từ 1 đến 28 có 28 số nguyên dương
Vậy có ít nhất 1 phân f tử thuộc A = 1 phần tử thuộc B