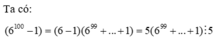So sánh: 5100 + 6100 và 7100
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ND
2
1 tháng 5 2022
umm, bn nhân A với 1/7 và nhân B với 1/9, sau đó tính ra và so sánh thôi
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
26 tháng 8 2023
Bài 1:
D = 5 + 52 + 53+...+ 5100
5.D = 52 + 53+...+5 100 + 5101
5D - D = 5101 - 5
4D = 5101 - 5
D = \(\dfrac{5^{101}-5}{4}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
26 tháng 8 2023
Bài 2:
So sánh
a, 544 = (2.33)4 = 24.312
2112 = (3.7)12 = 312.712
Vì 24 < 712 nên 544 < 2112
b, 339 và 1121
339 = (313)3
1121 = (117)3
313 = (32)6.3 = 96.3 < 97 < 117
Vậy 339 < 1121
ND
Nguyễn Đức Trí
VIP
26 tháng 8 2023
1) \(D=5+5^2+5^3+...+5^{100}\)
\(\Rightarrow D+1=1+5+5^2+5^3+...+5^{100}\)
\(\Rightarrow D+1=\dfrac{5^{100+1}-1}{5-1}\)
\(\Rightarrow D+1=\dfrac{5^{101}-1}{4}\)
\(\Rightarrow D=\dfrac{5^{101}-1}{4}-1=\dfrac{5^{101}-5}{4}=\dfrac{5\left(5^{100}-1\right)}{4}\)
2)
a) \(21^{12}=\left(21^3\right)^4=9261^4>54^4\Rightarrow54^4< 21^{12}\)
b) \(3^{39}< 3^{40}=\left(3^2\right)^{20}=9^{20}< 11^{20}< 11^{21}\)
\(\Rightarrow3^{39}< 11^{21}\)
c) \(201^{60}=\left(201^4\right)^{15}=\text{1632240801}^{15}\)
\(398^{45}=\left(398^3\right)^{15}=\text{63044792}^{15}< \text{1632240801}^{15}\)
\(201^{60}>398^{45}\)
BD
14 tháng 8 2023
\(a,16^{19}=\left(2^4\right)^{19}=2^{76}\\ 8^{25}=\left(2^3\right)^{25}=2^{75}\)
Vì \(2^{76}>2^{75}=>16^{19}>8^{25}\)
b,\(3^{500}=\left(3^5\right)^{100}=243^{100}\)
Vì \(243^{100}>5^{100}=>3^{500}>5^{100}\)
CM
3 tháng 9 2019
Sơ đồ con đường |
Lời giải chi tiết |
|
Ta có: ( 6 100 − 1 ) = ( 6 − 1 ) ( 6 99 + ... + 1 ) = 5 ( 6 99 + ... + 1 ) ⋮ 5 |
4 tháng 3 2021
Đặt \(A=6^2+6^4+6^6+...+6^{98}+6^{100}\)
Ta có: \(A=6^2+6^4+6^6+...+6^{98}+6^{100}\)
\(\Leftrightarrow36A=6^4+6^6+...6^{100}+6^{102}\)
\(\Leftrightarrow A-36A=6^2+6^4+6^6+...6^{98}+6^{100}-6^4-6^6-...-6^{100}-6^{102}\)
\(\Leftrightarrow-35\cdot A=6^2-6^{102}\)
\(\Leftrightarrow A=\dfrac{6^{102}-6^2}{35}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
22 tháng 8 2023
C = 1 + 6 + 62+ 63+...+ 6100
6C = 6 + 62+ 63 +...+ 6100 + 6101
6C - C = 6101 - 1
5C = 6101 - 1
C = \(\dfrac{6^{101}-1}{5}\)
ND
Nguyễn Đức Trí
VIP
22 tháng 8 2023
\(C=1+6+6^2+...+6^{100}\)
\(\Rightarrow C=\dfrac{6^{100+1}-1}{6-1}\)
\(\Rightarrow C=\dfrac{6^{101}-1}{5}\)
CM
31 tháng 8 2018
230 + 4 + 3 10 + 7 100 = 230 + 4 + 0 , 3 + 0 , 07 = 230 + 4 , 37 = 234 , 37