K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 5 2022
a: \(F\left(x\right)=x^3+2x^2+3x+4\)
\(G\left(x\right)=x^3-x^2+3x+1\)
b: \(F\left(x\right)+G\left(x\right)=2x^3+x^2+6x+5\)
\(F\left(x\right)-G\left(x\right)=3x^2+3\)
20 tháng 8 2019
a) Ta có:
f(0) = -2.03 + 3.02 - 0 + 5 = 0 + 0 - 0 + 5 = 5
g(-1) = 2.(-1)3 - 2.(-1)2 + (-1) - 9 = -2 - 2 - 1 - 9 = -14
b) f(x) + g(x) = (-2x3 + 3x2 - x + 5) + (2x3 - 2x2 + x - 9)
= -2x3 + 3x2 - x + 5 + 2x3 - 2x2 + x - 9
= (-2x3 + 2x3) + (3x2 - 2x2) - (x - x) + (5 - 9)
= x2 - 4
f(x) - g(x) = (-2x3 + 3x2 - x + 5) - (2x3 - 2x2 + x - 9)
= -2x3 + 3x2 - x + 5 - 2x3 + 2x2 - x + 9
= -(2x3 + 2x3) + (3x2 + 2x2) - (x + x) + (5 + 9)
= -4x3 + 5x2 - 2x + 14
Các bạn giúp mk giải ý f, g vs ạ
25 tháng 7 2021
a) Ta có: \(A=\dfrac{x^2+x}{x^2-2x+1}:\left(\dfrac{x+1}{x}-\dfrac{1}{1-x}+\dfrac{2-x^2}{x^2-x}\right)\)
\(=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}:\dfrac{x^2-1+x+2-x^2}{x\left(x-1\right)}\)
\(=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}\cdot\dfrac{x\left(x-1\right)}{x+1}\)
\(=\dfrac{x^2}{x-1}\)
b) Ta có: |2x-5|=3
\(\Leftrightarrow\left[{}\begin{matrix}2x-5=-3\\2x-5=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=2\\2x=8\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\left(loại\right)\\x=4\left(nhận\right)\end{matrix}\right.\)
Thay x=4 vào A, ta được:
\(A=\dfrac{4^2}{4-1}=\dfrac{16}{3}\)
NK
1
TM
19 tháng 1 2022
a. \(y\text{×}\dfrac{1}{5}-\dfrac{2}{3}=\dfrac{1}{4}\)
\(y\text{×}\dfrac{1}{5}=\dfrac{1}{4}+\dfrac{2}{3}\)
\(y=\dfrac{11}{12}:\dfrac{1}{5}=\dfrac{55}{12}\)
b. \(\dfrac{8}{5}-y:\dfrac{1}{2}=1\)
\(y:\dfrac{1}{2}=\dfrac{8}{5}-1\)
\(y=\dfrac{6}{5}\)
c. \(y\text{×}\dfrac{3}{4}+y\text{×}\dfrac{1}{4}-y=99\)
\(y\text{×}\left(\dfrac{3}{4}+\dfrac{1}{4}-1\right)=99\)
\(y\text{×}0=99\) (vô lí)
=> Không có giá trị y nào thỏa mãn.
d. \(\dfrac{y}{2}+\dfrac{y}{3}+\dfrac{y}{6}=1\)
\(\dfrac{3\text{×}y+2\text{×}y+y}{6}=\dfrac{6}{6}\)
\(\Rightarrow3\text{×}y+2\text{×}y+y=6\)
\(y\text{×}\left(3+2+1\right)=6\) hay \(y\text{×}6=6\)
\(y=1\)
e. \(\dfrac{y}{2}-\dfrac{7}{3}=\dfrac{1}{6}\)
\(\dfrac{y}{2}=\dfrac{1}{6}+\dfrac{7}{3}=\dfrac{5}{2}\)
\(y=5\)
f. \(\dfrac{15}{y-2}=\dfrac{3}{7}\)
\(\dfrac{15}{y-2}=\dfrac{15}{35}\) \(\Rightarrow y-2=35\)
\(y=37\)
Các bài g, h còn lại bạn làm tương tự như bài f.
10 tháng 4 2019
f(2)=g(0)
=> c=5
f(1)=g(1)
=> a+b+c=2 mà c=5 => a+b=-3 (1)
f(-1)=g(3)
=>9a+3b+c=2 mà c=5= > 9a+3b=-3=> 3a+b=-1(2)
(2)-(1) ta được:
2a=2=>a=1=> b=-4
VẬy g(x)=x^2-4x+5
t i ck ủng hộ tui nha
1 tháng 6 2019
Ta có : G(0) = a.02 + b.0 + c = 4
=> c = 4
G(1) = a.12 + b.1 + c = 9
=> a + b + c = 9
Mà c = 4 => a + b = 9 - 4 = 5 (1)
G(2) = a.22 + b.2 + c = 14
=> 4a + 2b + c = 14
Mà c = 4 > 4a + 2b = 14 - 4 = 10 => 2a + b = 5 (2)
Từ (1) và (2) trừ vế cho vế :
(a + b) - (2a + b) = 5 - 5
=> -a = 0 => a = 0
Thay a = 0 vào (1), ta được : 0 + b = 5 => b = 5
Vậy ...
1 tháng 6 2019
\(G\left(0\right)=4\Rightarrow a.0^2+b.0+c=c=4\)
\(G\left(1\right)=9\Rightarrow a.1^2+b.1+c=a+b=9\)
\(G\left(2\right)=14\Rightarrow a.2^2+b.2+c=4a+2b=2.\left(2a+b\right)=14\)
\(\Rightarrow2a+b=7\)
Ta có: 2a + b - (a + b) = a = -2
=> b = 9 - (-2) = 11
Vậy a = -2; b = 11; c = 0
15 tháng 4 2018
ta có: f(x) + g(x) = ( 7 x^6 - 6x ^5 +5x^4 -4x^3 +3x^2 -2x +1) - ( x - 2x^2 +3x^3 - 4x^4 + 5x^5 - 6x^6)
\(=7x^6-6x^5+5x^4-4x^3+3x^2-2x+1-x+2x^2-3x^3+4x^4-5x^5+6x^6\)
\(=\left(7x^6+6x^6\right)-\left(6x^5+5x^5\right)+\left(5x^4+4x^4\right)-\left(4x^3+3x^3\right)+\left(3x^2+2x^2\right)-\left(2x+x\right)+1\)
\(=13x^6-11x^5+9x^4-7x^3+5x^2-3x+1\)
Chúc bn học tốt !!!!!!
TN
Tống Ngọc Châu
VIP
4 tháng 12 2021
Uhhhhhhhhhhhhhhhhhhhhhhhhhh😥😥😥😥😥😥😥😥😥😥😥????????????...............
7 tháng 5 2018
Cho f(x) = 0
=> ( x -2 ).( x+3) = 0
=> x -2 = 0 => x= 2
x + 3 = 0 => x = - 3
=> x =2 , x = -3 là nghiệm của f(x)
mà nghiệm của f(x) cũng là nghiệm của g(x)
=> x = 2; x = -3 là nghiệm của g(x)
ta có: x = 2 là nghiệm của g(x)
=> 2^3 + a. 2^2 + b. 2 + 2 = 0
8 + 4a + 2b + 2 = 0
2.( 4 + 2a + b + 1) =0
=> 4 + 2a + b + 1 = 0
2a + b + 5 = 0
b = -5 - 2a
ta có: x = -3 là nghiệm của g(x)
=> (-3)^3 + a . ( -3)^2 + b.(-3) + 2 = 0
- 27 + 9a - 3b + 2 = 0
- 25 + 9a - 3.( -5 - 2a) = 0
- 25 + 9a + 15 + 6a = 0
-10 + 15 a = 0
15a = 10
a = 10 / 15
a = 2/3
mà b = -5 - 2a
b = -5 - 2. 2/3
b = - 5 - 4/ 3
b = -19/3
KL: a = 2/3, b = -19/3
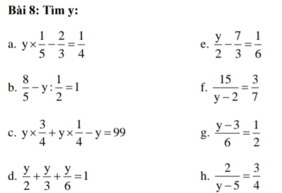
\(f,x^2-2\sqrt{5}x+5=0\)
\(\left(x-\sqrt{5}\right)^2=0\)
\(x-\sqrt{5}=0\)
\(x=\sqrt{5}\)
\(g,\sqrt{x^2-4x+4}-\sqrt{x^2+2x+1}=-3\)
\(\sqrt{\left(x-2\right)^2}-\sqrt{\left(x+1\right)^2}=-3\)
\(\left|x-2\right|-\left|x+1\right|=-3\)
lập bảng xét dấu:
\(TH1:x\le-1\)
\(2-x+x+1=-3\)
\(3=-3\left(KTM\right)\)
\(TH2:-1< x\le2\)
\(2-x-x-1=-3\)
\(2x=4\)
\(x=2\left(TM\right)\)
\(TH3:x>2\)
\(x-2-x-1=-3\)
\(0x=0\)
pt vô số n0 kết hợp với đkxđ
\(x>2\)