giải BPT sau rồi biểu diễn tập nghiệm trên trục số
x + 2 / x - 3 < 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H
14 tháng 5 2023
`(x-2)/6 -(x-1)/3 < x/2`
`<=> (x-2)/6 -(2(x-1))/6 < (3x)/6`
`<=> x-2 - (2x-2) <3x`
`<=> x-2-2x+2<3x`
`<=> -x <3x`
`<=> -x-3x<0`
`<=> -4x<0`
`<=> x>0`
NN
23 tháng 4 2016
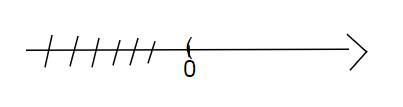
a) |x-7|=2x+3 (1)
Ta có:|x-7|=x-7<=>x-7 \(\ge\) 0<=>x\(\ge\)7
|x-7|=-(x-7)<=>x-7<0<=>x<7
Nếu x\(\ge\) 7thì (1) <=>x-7=2x+3
<=>x-2x=7+3
<=>-x = 10
<=>x=-10 (ko thỏa mãn đk)
Nếu x<7 thì (1) <=>-(x-7)=2x+3
<=>-x+7=2x+3
<=>-x-2x=-7+3
<=>-3x=-4
<=>x=4/3 (thỏa mãn đk)
còn câu b nx ạ. Giupp mình vs. Mình cammon nhiuu
ND
25 tháng 4 2018
a) \(x^2-4x+3\ge0\)
\(\Leftrightarrow x^2-3x-x+3\ge0\)
\(\Leftrightarrow x\left(x-3\right)-\left(x-3\right)\ge0\)
\(\Leftrightarrow\left(x-3\right)\left(x-1\right)\ge0\)
* \(x-3\ge0\) và \(x-1\ge0\)
\(\Leftrightarrow x\ge3\) và \(x\ge1\)
\(\Leftrightarrow x\ge3\)
* \(x-3\le0\) và \(x-1\le0\)
\(\Leftrightarrow x\le3\) và \(x\le1\)
\(\Leftrightarrow x\le1\)
Vậy \(x\ge3\) và \(x\le1\)
26 tháng 4 2018
b) x3 - 2x2 + 3x - 6 < 0
⇔ x2( x - 2 ) + 3( x - 2) < 0
⇔ ( x - 2)( x2 + 3) < 0
Do : x2 + 3 > 0 ∀x
⇒ x - 2 < 0
⇒ x < 2
KL....
10 tháng 4 2018
a) 1,2x < -6
\(\Leftrightarrow1,2x.\dfrac{1}{1,2}< -6.\dfrac{1}{1,2}\)
\(\Leftrightarrow\) \(\dfrac{1,2x}{1,2}< \dfrac{-6}{1,2}\)
\(\Leftrightarrow x< -5\)
Vậy nghiệm của BPT là : \(x< -5\)
b) \(3x+4>2x+3\)
\(\Leftrightarrow3x-2x>-4+3\)
\(\Leftrightarrow x>-1\)
Vậy nghiệm của BPT là : \(x>-1\)
c) \(2x-3>0\)
\(\Leftrightarrow2x>3\)
\(\Leftrightarrow2x.\dfrac{1}{2}>3.\dfrac{1}{2}\)
\(\Leftrightarrow x>1,5\)
Vậy nghiệm của BPT là : \(x>1,5\)
d) \(4-3x\le2\)
\(\Leftrightarrow-3x\le2-4\)
\(\Leftrightarrow-3x\le-2\)
\(\Leftrightarrow-3x.\dfrac{-1}{3}\ge-2.\dfrac{-1}{3}\)
\(\Leftrightarrow x\ge\dfrac{2}{3}\)
Vậy tập nghiệm của BPT là : \(x\ge\dfrac{2}{3}\)
Ta có: \(\dfrac{x+2}{x-3}< 0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+2>0\\x-3< 0\end{matrix}\right.\Leftrightarrow-2< x< 3\)
Vậy: S={x|-2<x<3}
2 trường hợp chứ em nhỉ !