Cho hàm số y=x2 có đồ thị là (P) và hai điểm M,N thuộc (P) có hoành độ lần lượt là -1 và 2.
a, Viết phương trình đường thẳng đi qua hai điểm M,N
b, Vẽ đồ thị (P) trên hệ trục tọa độ Oxy và tìm tọa độ điểm E thuộc đoạn đường cong MN của đồ thị (P) sao cho ΔMNE có diện tích lớn nhất

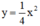
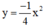
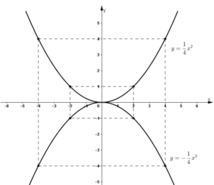
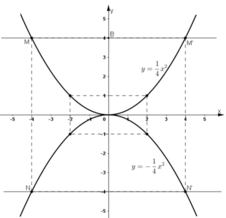
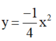 tại N và N’.
tại N và N’.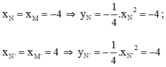
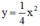
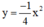

a) Thay x=-1 vào (P), ta được:
\(y=\left(-1\right)^2=1\)
Thay x=2 vào (P), ta được:
\(y=2^2=4\)
Vậy: M(-1;1) và N(2;4)
Gọi (d):y=ax+b là ptđt đi qua hai điểm M và N
\(\Leftrightarrow\left\{{}\begin{matrix}-a+b=1\\2a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3a=-3\\-a+b=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=1\\b-1=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\)
Vậy: (d): y=x+2