tìm GTLN và GTNN của hàm số sau \(y=3\sin x+4\cos x+1\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
6 tháng 8 2021
2.
$y=\sin ^4x+\cos ^4x=(\sin ^2x+\cos ^2x)^2-2\sin ^2x\cos ^2x$
$=1-\frac{1}{2}(2\sin x\cos x)^2=1-\frac{1}{2}\sin ^22x$
Vì: $0\leq \sin ^22x\leq 1$
$\Rightarrow 1\geq 1-\frac{1}{2}\sin ^22x\geq \frac{1}{2}$
Vậy $y_{\max}=1; y_{\min}=\frac{1}{2}$
AH
Akai Haruma
Giáo viên
6 tháng 8 2021
3.
$0\leq |\sin x|\leq 1$
$\Rightarrow 3\geq 3-2|\sin x|\geq 1$
Vậy $y_{\min}=1; y_{\max}=3$
A
1
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
a.
\(-1\le sin\left(1-x^2\right)\le1\)
\(\Rightarrow y_{min}=-1\) khi \(1-x^2=-\dfrac{\pi}{2}+k2\pi\) \(\Rightarrow x^2=\dfrac{\pi}{2}+1+k2\pi\) (\(k\ge0\))
\(y_{max}=1\) khi \(1-x^2=\dfrac{\pi}{2}+k2\pi\Rightarrow x^2=1-\dfrac{\pi}{2}+k2\pi\) (\(k\ge1\))
b.
Đặt \(\sqrt{2-x^2}=t\Rightarrow t\in\left[0;\sqrt{2}\right]\subset\left[0;\pi\right]\)
\(y=cost\) nghịch biến trên \(\left[0;\pi\right]\Rightarrow\) nghịch biến trên \(\left[0;\sqrt{2}\right]\)
\(\Rightarrow y_{max}=y\left(0\right)=cos0=1\) khi \(x^2=2\Rightarrow x=\pm\sqrt{2}\)
\(y_{min}=y\left(\sqrt{2}\right)=cos\sqrt{2}\) khi \(x=0\)
LT
1
TM
1
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 10 2021
Đề là \(\dfrac{cos^2x}{3}+\dfrac{sinx}{3}+1\) hay \(cos^2\left(\dfrac{x}{3}\right)+sin\left(\dfrac{x}{3}\right)+1\) vậy nhỉ?
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 7 2021
24.
\(cos\left(x-\dfrac{\pi}{2}\right)\le1\Rightarrow y\le3.1+1=4\)
\(y_{max}=4\)
26.
\(y=\sqrt{2}cos\left(2x-\dfrac{\pi}{4}\right)\)
Do \(cos\left(2x-\dfrac{\pi}{4}\right)\le1\Rightarrow y\le\sqrt{2}\)
\(y_{max}=\sqrt{2}\)
b.
\(\dfrac{1}{2}sinx+\dfrac{\sqrt{3}}{2}cosx=\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x-\dfrac{\pi}{6}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{6}=\dfrac{\pi}{3}+k2\pi\\x-\dfrac{\pi}{6}=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k2\pi\\x=-\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
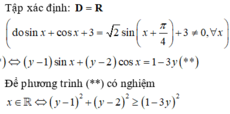
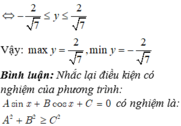
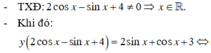
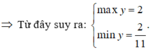
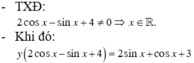
Lời giải
Áp dụng BĐT (ac+bd)2≤(c2+d2)(a2+b2) .
Đẳng thức xảy ra khi ac=bd .
Ta có: (3sinx+4cosx)2≤(32+42)(sin2x+cos2x)=25
⇒–5≤3sinx+4cosx≤5⇒–4≤y≤6 .
Vậy maxy=6 , đạt được khi tanx=34 .
miny=–4 , đạt được khi tanx=–34 .
Dùng \(asinx+b.cosx=c\) cũng được :
C 2 : \(y-1=3sinx+4cosx\) ( * )
( * ) có no \(\Leftrightarrow3^2+4^2\ge\left(y-1\right)^2\Leftrightarrow\left(y-1\right)^2\le25\)
\(\Leftrightarrow-5\le y-1\le5\)
\(\Leftrightarrow-4\le y\le6\)
Xét Min \(y=-4\) ; ta có : \(3sinx+4cosx+1=-4\)
\(\Leftrightarrow3sinx+4cosx=-5\)
Đến đây ; xét cos x = 0 hoặc cos x khác 0 ; rồi chia cho cos^2 x ; tìm được x ( bn tự làm )
Xét Max \(y=6\) ; làm tương tự như trên