Trên một đoàn tàu hỏa, phụ trách một toa tàu thông báo trong toa có một số người bị nhọ mặt và ra hiệu lệnh: Mọi người tập hợp xung quanh tôi, không được soi gương, nói chuyện hay bất kỳ hành động nào có thể giúp cho người khác biết về tình trạng nhọ hay không nhọ. Chỉ được phép nhìn nhau và suy nghĩ, nếu ai biết chắc chắn mình bị nhọ thì khi tàu dừng sẽ xuống rửa. Kết quả là sau khi tàu dừng ở ga thứ 4 thì không còn ai bị nhọ. Hỏi ban đầu trong toa tàu có bao nhiêu người bị nhọ mặt?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4 người, suy luận như sau:
-Nếu có 1 người -> người đó thấy ko ai dính nhọ nên biết chắc là mình -> sẽ đi rửa ở lần đầu tiên. Vậy có nhiều hơn 1 người.
-Nếu có 2 người -> mỗi người sẽ thấy 1 người dính nhọ. Khi đó lần 1 ko có ai đi rửa do người này cứ nghĩ chỉ có người kia dính . Sau khi tàu chạy , họ sẽ thấy người kia vẫn còn nhọ nên biết chắc là trên toa còn người khác dính nữa, sẽ suy ra được bản thân mình là người dính. Vậy cả 2 sẽ đi rửa ở lần 2. Vậy có nhiều hơn 2 người dính nhọ.
-Suy luận tương tự , nếu 3 người thì 2 lần đầu sẽ ko có ai rửa vì ai cũng suy luận như trên, và sau đó sẽ biết mình bị nhọ, lúc đó sẽ đi rửa ở lần 3.
-Với 4 người thì cũng suy như thế -> đi rửa ở lần 4.
-Vậy đáp án có 4 người bị nhọ
4 người, suy luận như sau:
-Nếu có 1 người -> người đó thấy ko ai dính nhọ nên biết chắc là mình -> sẽ đi rửa ở lần đầu tiên. Vậy có nhiều hơn 1 người.
-Nếu có 2 người -> mỗi người sẽ thấy 1 người dính nhọ. Khi đó lần 1 ko có ai đi rửa do người này cứ nghĩ chỉ có người kia dính . Sau khi tàu chạy , họ sẽ thấy người kia vẫn còn nhọ nên biết chắc là trên toa còn người khác dính nữa, sẽ suy ra được bản thân mình là người dính. Vậy cả 2 sẽ đi rửa ở lần 2. Vậy có nhiều hơn 2 người dính nhọ.
-Suy luận tương tự , nếu 3 người thì 2 lần đầu sẽ ko có ai rửa vì ai cũng suy luận như trên, và sau đó sẽ biết mình bị nhọ, lúc đó sẽ đi rửa ở lần 3.
-Với 4 người thì cũng suy như thế -> đi rửa ở lần 4.
-Vậy đáp án có 4 người bị nhọ

Số cách lên toa của 7 người là: 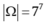
Ta tìm số khả năng thuận lợi của A như sau
Chọn 3 toa có người lên: ![]()
Với toa có 4 người lên ta có: ![]() cách chọn
cách chọn
Với toa có 2 người lên ta có: ![]() cách chọn
cách chọn
Người cuối cùng cho vào toa còn lại nên có 1 cách
Theo quy tắc nhân ta có: ![]()
Do đó: 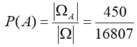 .
.
Chọn A.

Một hành khách khi đến ga thì thấy toa sát cuối của đoàn tàu anh ta cần lên đã chuyển động nhanh dần đều qua trước mặt mình trong thời gian t1 = 10s, còn toa cuối qua trong thời gian t2 = 8s. Hỏi người này bị chậm so với giờ tàu khởi hành là bao lâu?
Giải:
gọi thời gian muộn là t,chiều dài mỗi toa tàu là l
Vận tốc của tàu khi toa áp chót bắt đầu đi qua người là a.t, ta có phương trình l = (1/2).a.t1^2 + a.t.t1(1)
Vận tốc của tàu khi toa áp chót bắt đầu đi qua người là a(t + t1), ta có phương trình l = (1/2).a.t2^2 + a(t + t1).t2 (2).
Từ (1) và (2) giải t = 31s

Chọn C
Chọn toa có 3 người có 3 (toa)
Chọn 3 hành khách xếp vào toa đó có ![]() (cách)
(cách)
Hành khách còn lại có 2 cách chọn toa
Số cách chọn là: 3. ![]() .2 = 24 (C).
.2 = 24 (C).

Người bị nhọ nhìn thấy mình bị người khác cười là người đấy bị nhọ.
Nhấn đúng cho mik nha.
n người bị nhọ mặt