Tìm tất cả các giá trị nguyên của m để hàm số : y = \(\dfrac{mx-2}{2x-m}\) đồng biến trên (-2;3] .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 6 2021
1.
\(y'=m-3cos3x\)
Hàm đồng biến trên R khi và chỉ khi \(m-3cos3x\ge0\) ; \(\forall x\)
\(\Leftrightarrow m\ge3cos3x\) ; \(\forall x\)
\(\Leftrightarrow m\ge\max\limits_{x\in R}\left(3cos3x\right)\)
\(\Leftrightarrow m\ge3\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 6 2021
2.
\(y'=1-m.sinx\)
Hàm đồng biến trên R khi và chỉ khi:
\(1-m.sinx\ge0\) ; \(\forall x\)
\(\Leftrightarrow1\ge m.sinx\) ; \(\forall x\)
- Với \(m=0\) thỏa mãn
- Với \(m< 0\Rightarrow\dfrac{1}{m}\le sinx\Leftrightarrow\dfrac{1}{m}\le\min\limits_R\left(sinx\right)=-1\)
\(\Rightarrow m\ge-1\)
- Với \(m>0\Rightarrow\dfrac{1}{m}\ge sinx\Leftrightarrow\dfrac{1}{m}\ge\max\limits_R\left(sinx\right)=1\)
\(\Rightarrow m\le1\)
Kết hợp lại ta được: \(-1\le m\le1\)
CM
14 tháng 7 2017
Đáp án C
Ta có: y ' = m − 2 x − 1 2
Hàm số đồng biến trên các khoảng xác định ⇔ y ' > 0 ⇔ m − 2 > 0 ⇔ m > 2
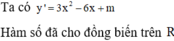
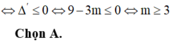
TXĐ: `D=RR \\ {m/2}`.
`y'=(m^2+4)/((2x-m)^2)`
Hàm số đồng biến trên `(-2;3] <=>` $\begin{cases}m^2+4>0 \forall m\\ \dfrac{m}{2} \notin (-2;3]\\\end{cases}$ `<=>` $\begin{cases}m>6\\m≤-4\\\end{cases}$
Vậy `m>6 \vee m <= -4` thỏa mãn.