Hai điện trở R1 và R2 được mắc vào một hiệu điện thế không đổi bằng cách ghép song song với nhau hoặc ghép nối tiếp với nhau. Gọi Pss là công suất tiêu thụ của đoạn mạch khi ghép song song, Pnt là công suất tiêu thụ khi ghép nối tiếp. Chứng minh: Pss/Pnt>=4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án: A
Khi hai điện trở ghép nối tiếp:
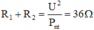
Khi hai điện trở ghép song song:
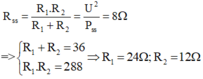

Đáp án: A
HD Giải: Khi mắc 2 điện trở nối tiếp: Rnt = R1 + R2, P n t = U 2 R 1 + R 2 ⇒ R 1 + R 2 = U 2 P = 12 2 4 = 36
Khi mắc 2 điện trở song song: R s s = R 1 R 2 R 1 + R 2 = R 1 R 2 36 ⇒ P s s = 36 U 2 R 1 R 2 ⇒ R 1 R 2 = 36 U 2 P = 288
R1 và R2 là nghiệm của phương trình R2 – 36R + 288 = 0 => R1= 24W; R2= 12W

a,cường độ dòng điện chạy qua mạch: \(I_{AB}=\dfrac{P}{U_{AB}}=\dfrac{36}{12}=3\left(A\right)\)
Gọi x là điện trở R2 (Ω)
2x là điện trở R1 (Ω)
\(R_{tđ}=\dfrac{R_1R_2}{R_1+R_2}=\dfrac{2x.x}{2x+x}=\dfrac{2x^2}{3x}\)
\(R_{tđ}=\dfrac{U_{AB}}{I_{AB}}=\dfrac{12}{3}=4\left(\Omega\right)\)
\(\Rightarrow\dfrac{2x^2}{3x}=4\Rightarrow x=6\left(\Omega\right)\)
Điện trở R1 = 2x = 12(Ω)
Điện trở R2 = x = 6 (Ω)
b, Gọi điện trở R3 là y (Ω)
Công suất tiêu thụ sau khi mắc thêm R3:
\(\dfrac{P}{4}=\dfrac{36}{4}=9\left(W\right)\)
Cường độ dòng điện chạy qua dây dẫn AB: \(I=\dfrac{P}{U}=\dfrac{9}{12}=0,75\left(A\right)\)
Vì là mạch nối tiếp nên \(U_{AB}=U_{12}=U_3=12V\)
\(R_{tđ}=\dfrac{R_1R_2}{R_1+R_2}+R_3=\dfrac{6.12}{6+12}+R_3=4+y\)
\(R_{tđ}=\dfrac{U_{AB}}{I_{AB}}=\dfrac{12}{0,75}=16\left(\Omega\right)\)
⇒ 4 + y = 16 \(\Rightarrow\) y = 12 (Ω)
Hay R3 = 12(Ω)


áp dụng \(P=UI=I^2R=\dfrac{U^2}{R}\) váo 2 điện trở mắc song song
trong hiệu điện thế ko đổi U
\(=>Pss=\dfrac{U^2}{Rtd}=\dfrac{U^2}{\dfrac{R1.R2}{R1+R2}}\)
áp dụng vào 2 điện trở nối tiếp
\(=>Pnt=\dfrac{U^2}{R1+R2}\)
\(=>\dfrac{Pss}{Pnt}=\dfrac{\dfrac{\dfrac{U^2}{R1R2}}{R1+R2}}{\dfrac{U^2}{R1+R2}}=\dfrac{\left(R1+R2\right)^2}{R1.R2}\)
do điện trở R1,R2 là các số không âm
áp dụng BDT cosi\(=>R1+R2\ge2\sqrt{R1.R2}\)
\(=>\left(R1+R2\right)^2\ge4R1.R2\)
\(=>\dfrac{\left(R1+R2\right)^2}{R1.R2}\ge4\)(dpcm)